Fraktaler er geometriske framstillinger av kaosdynamikk, fingeravtrykkene til kaos. Fraktaler viser selvsimilaritet hvor et lite mønster gjenfinnes i det store. Skyformasjoner, bregnefronder, greining i trær og Romanesco-kål (Brassica oleracea cv. Romanesco) er eksempler på naturlige fraktaler.

Andre eksempler på fraktaler er banefraktaler: Mandelbrotmengden, Julia-mengden, Lyapunov-mengden. Itererte fraktaler: von Koch´s snøflak, Cantor-mengde, Peanokurver, Sierpinskitriangel og Mengersvamp, samt tilfeldige fraktaler: Brownske fraktaler.

Julia-mengden er iterasjoner i kompleksplanet:
\(\displaystyle Z= X + Yi\;\;\;\;\, C= A+ Bi\;\;\;\;\; Z_ {n+1}= Z_n^2+ C\)
Mandelbrotmengde:
\(\displaystyle X_ {n+1}= X_n^2-Y_n^2+ A\;\;\;\;\;\; Y_{n+1}= 2X_nY_n+ B\)
Fraktaler kan enten være deterministiske eller eksakt geometriske (selvsimilare) eller de kan være tilfeldige statistiske selvsimilare. Barnsleys boktittel Fractals everywhere (1988) henspeiler på at man kan finne fraktale mønstre overalt i naturen: bregneblad (Maichael F. Barnsley 1985), romanescokål, fjær, greining på trær, mønster i ytterbarken på trær, fjell, fossende vann og vannvirvler, form på skyer, luftkanalene i en menneskelunge,meslingvirusutbrudd, aksjekurser osv.

Måler man lengden av norskekysten vil lengden av kysten variere med hvilken målestokk man bruker, kalt Richardson effekt (kystlinjeparadokset) oppkalt etter Lewis Fry Richardson (1881-1953). En mindre målestokk er mer følsom, og lengden går uendelig når målestokken går mot null. Richardson fant også at antall kriger er proporsjonalt med antall land det grenser til.
En linje, et kvadrat og en kube har henholdsvis dimensjon 1, 2 og 3.
Hvis man har en firkant som skal bli dobbelt så stor så trengs 4 kopier (22). Skal den bli tre ganger så stor så trengs 9 kopier(32).
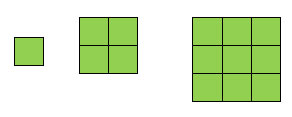
Generelt hvis man trenger N kopier av et objekt for å lage et objekt som skal oppskaleres til størrelse S så kalles d dimensjonen som gir sammenhengen:
\(\displaystyle S^d=N \;\;\;\;\;d=\frac{\ln N}{\ln S}\)
For et plan er d=2, tredimensjonalt blir d=3 og for en linje blir d=1.
Fraktale dimensjoner er verken 1, 2 eller 3.
Hvis kystlinjen har totallengde L og målestokken er ε så blir L(ε)= ε/εd, hvor d=1.26 for kysten av Storbritannia.
Cantor-mengde
En Cantor-mengde (G.F.L.P. Cantor (1845-1918) består av en initiatorlinje hvor den midtre linjen i intervallet 1/3-2/3 fjernes, og det dannes en generatorlinje med to linjesegmenter som angir mønsteret for resten av fraktalen. Cantor-mengden (Cantor-støv) er en fraktal og viser selvsimilaritet, hver linje er lik den forrige, men har bare 1/3 av lengden osv.

Hvert stykke er atskilt med et gap. Lengden etter et trinn er 2/3 av lengden etter forrige trinn slik at den totale lengden minsker med (2/3)n, hvor n er antall trinn.
Cantor-mengde har fraktal dimensjon 3d=2 dvs. d=ln2/ln3=0.63….
Koch-kurve
En Koch-kurve (Koch-snøflak), navn etter den svenske matematikeren Niels Fabian Helge von Koch(1870-1924), er en fraktal. Starter med en linje som splittes i tre like deler, og hvor linjestykke fra 1/3-2/3 fjernes og erstattes med to linjer med samme lengde som 1/3 av den opprinnelige lengden, slik at de danner en V-form, og man har i alt 4 linjer. Deretter splittes hver av de fire linjene i tre deler, den midterste erstattes av to nye 1/3 lange linjer, og slik fortsetter iterasjonene:
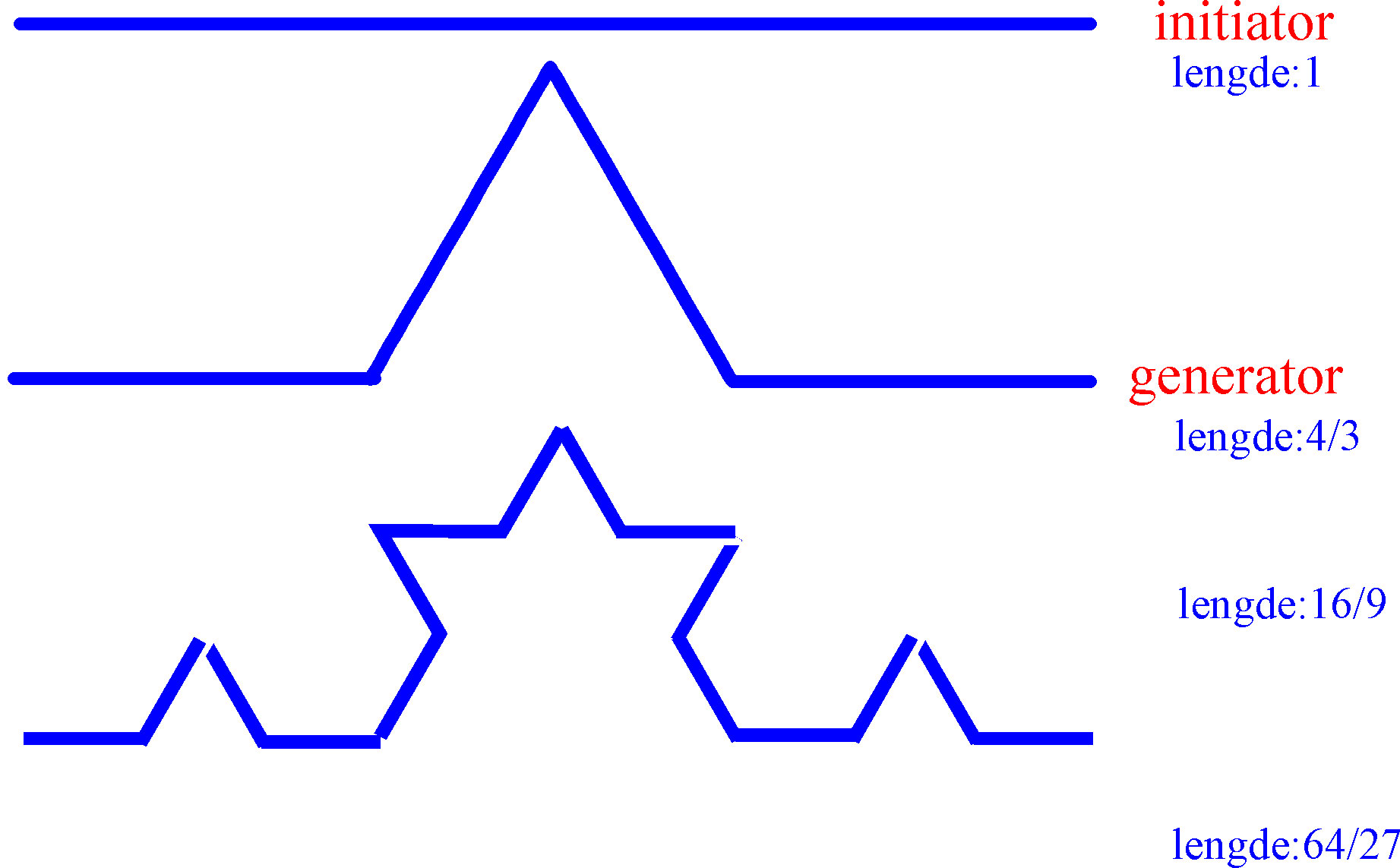
Koch-kurven har fraktaldimensjonen 3d=4 dvs. d=ln4/ln3= 1.2618….
Hvis man starter med en initiator med lengde 1 cm, så vokser lengden med (4/3)n, hvor n er antall iterasjoner.
Selv om Koch-kurven er kontinuerlig er den ikke deriverbar. Arealet som Koch-kurven er endelig med areal:
\(\displaystyle \frac{2 \sqrt{3}\;x^2}{5}\)
hvor x er sidelengden.
Hvis vi plotter logaritmen til lengden logY=log(1,4/9, 16/9,64/27,…) versus logaritmen til målestokken log(X)= log(1,1/3,1/9,1/27…) for en Koch-kurve. Stigningskoeffisienten til linjen=1-d, hvor d er fraktal dimensjon.
\(\log (\text{lengden})=(1-d)\log(\text{målestokk}+ \beta)\)
Den totale lengden av Koch-kurven blir lik 3∙(4/3)n etter n trinn.
Sierpinskitriangel
Et Sierpinskitriangel er en fraktal som baserer seg på slumpvandring mellom tre punkter A, B og C som danner en trekant. Det hele starter i et punkt (x0)og så trekker man tilfeldig ut A, B eller C (for eksempel ved myntkast) og trekker en rett linje halvveis mot punktet man har valgt. Dette gjentas og gjentas (iterasjoner).

Dimensjonen d er:
\(\displaystyle d=\frac{\log(\text{antall trekanter})}{\log(\text{forstørrelse})}=\frac{\log 3}{\log 2}=1.584 \dots\)
Et Sierpinski-triangel har fraktaldimensjon 2d=3 dvs. d=ln3/ln2=1.5849…
Mengersvamp er en fraktal hvor antall kuber er 20, og n er antall iterasjoner av en første kuben. Et tenkt utgangspunkt er en standard Rubiks kube hvor den midterste kuben på hver side fjernes. Deretter lages det hull i midten av de gjenværende kubene, og dette gjentas og gjentas. Mengersvamp (Karl Menger 1902-1985) består av et uendelig antall hulrom og er en fraktal. Starten på Mengersvampen er en kube bestående av 3∙3∙3=27 småkuber som i Rubiks kube. Fjern midtkuben og de seks småkubene som vender mot den, og man har da igjen 20 småkuber. Del de 20 småkubene i nye 3∙3∙3=27 enda mindre kuber, fjern midtkuben og de 6 som vender mot dem i alle sammen, gjenta interasjonsprosessen. Antall kuber øker med 20n hvor n er antall iterasjoner. Allerede etter 2 iterasjoner er det 400 småkuber, etter 6 iterasjoner er det 64 millioner osv. Hver sideflate i en Mengersvamp er et Sierpinskiteppe. Mengersvampen har Hausdorffdimensjon 2.73, et mål på fraktaldimensjon (Felix Hausdorff 1868-1942).