Gjentatte Bernoulli-eksperimenter følger en binomial fordeling hvor det bare er to mulige utfall. Til slutt og nederst faller kulene ned i atskilte brønner. Det er større sannsynlighet for at en kule treffer en hindring i midten av brettet enn i ytterkantene, og det er flere muligheter nær midten. Brettet kan lages med tre- eller metall-pigger på en glatt plate for eksempel en treplate.
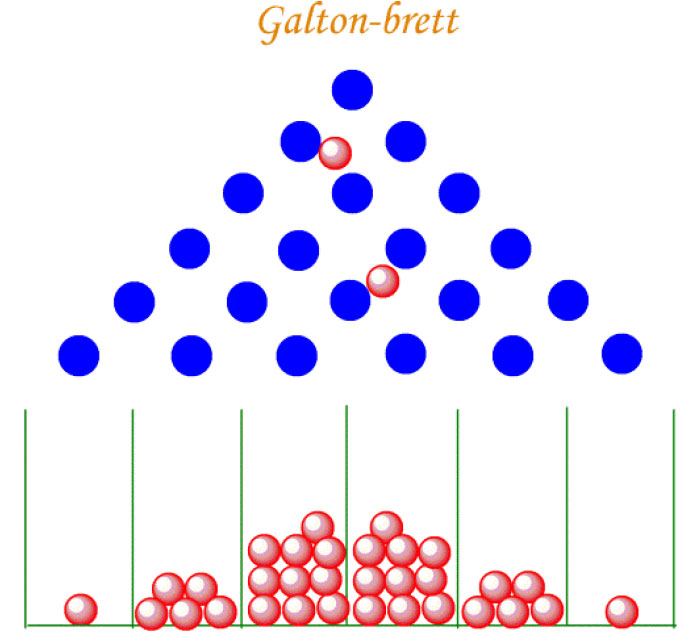
Galton-brett. Jo flere veier en kule har mulighet til å velge, desto nærmere sentrumsbrønnen havner den. P(x) er sannsynligheten for et gitt utfall. Det betyr at kulen har størst sannsynlighet for å havne i brønn 2-4 på figuren, altså blant de midterste.
Det interessante er at normalfordelingen kommer naturlig som et estimat fra en kombinasjon av et stort antall uavhengige hendelser. Dette er et resultat av sentralgrenseteoremet. Gjennomsnittet av et stort antall uavhengige hendelser, som ikke nødvedigvis må følge normalfordelingen, i Galton-brett følges den diskrete binomialfordelingen, men kulene i brønnene følger tilnærmet den kontinuerlige normalfordelingen. Det skyldes av for en stor verdi av n for en binomial variabel med utfall p=0.5 så vil denne ha samme form som normalfordelingen, det vil si med ca. samme gjennomsnitt og standardavvik
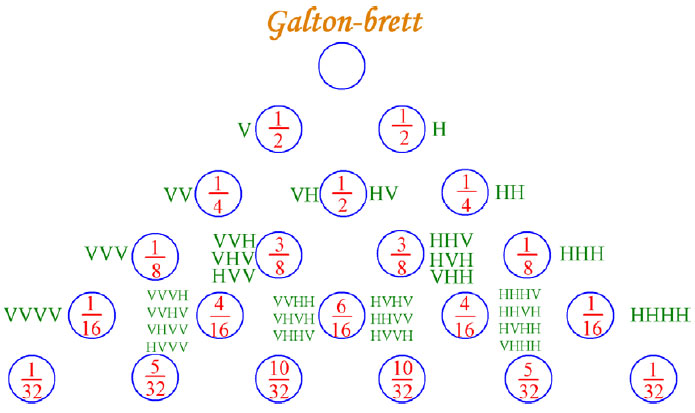
V-ventre og H-Høyre. Figuren viser mulighetene ved hver hindring. Man ser at tallene som går igjen er tallene i Pascals trekant. Det er flere mulige veier å velge for kulen i midten av brettet.
For den nederste rekken er det ikke satt opp de mulige utfallene, men tallene som dukker opp før kulene faller ned i brønnene på bunnen av brettet blir for de 26=64 mulige utfallene:
1/64, 6/64, 15/64, 20/64, 15/64, 6/64 , 1/64
hvor 1+6+15+20+15+6+1=64
Vi definerer fakultetsfunksjonen n! (n fakultet):
\(n!=n(n-1)(n-2)(n-3)\dots 3\cdot 2 \cdot 1\)
\(0!=1\)
Det er bare en måte å ordne null objekter.
Fakultetsfunksjonen gjelder bare for positive heltall. Det er bare når n=0 og n=1 at n! blir et oddetall, ellers blir det alltid et liketall, og den øker meget raskt med n. Tallene for n-fakultet for tallene 0 til 12:
1 1 2 6 24 120 720
5040 40320 362880 3628800 39916800 479001600
Fakultetsfunksjonen kan også uttrykkes som produktnotasjon:
\(n!=\displaystyle\prod_{k=1} ^n k\)
Når man regner ut binomialkoeffisienten benyttes fakultetsfunksjonen:
\(\frac{n!}{k!(n-k)!} = \binom{n}{k} \;\;\;\;\;\; k<n\)
Binomialkoeffisientene kan settes opp i Pascals trekant, hvor tallene i neste horisontale linje er summen av de ovenfor og havner midt mellom dem.
Fig
Trekanten er symmetrisk om midtlinjen og:
\(\binom{n}{x}=\binom{n}{n-x}\)

De tilsvarende tallene satt opp som binomialkoeffisienter

Flere av tallene i Pascals trekant:

Myntkast og simulering av et Galton-brett
Vi kan simulere et Galton-brett som har seks rader med pinner ved å kaste en mynt 6 ganger. Blir det kron (suksess) går man til høyre (H) og blir det mynt (ikke-suksess) går man til venstre (V). Et mulig utfall er følgende 4 til høyre og 2 til venstre (tilsvarende 4 kron)
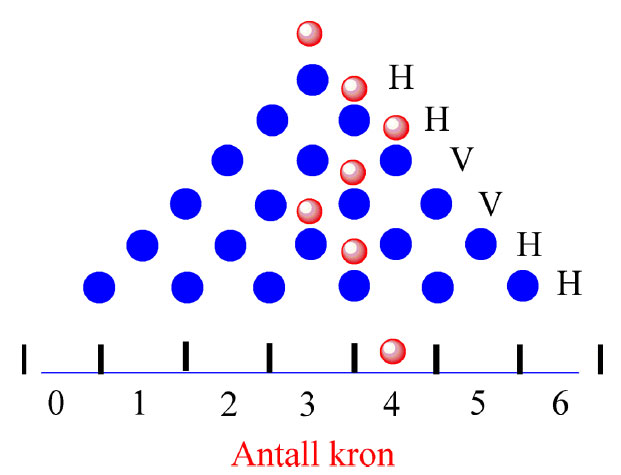
Vi kan simulere et Galton-brett ved å kaste en mynt 6 ganger. Blir det kron (suksess) går man til høyre (H) og blir det mynt (ikke-suksess) går man til venstre (V). Et mulig utfall er følgende 4 til høyre og 2 til venstre (tilsvarende 4 kron)
Binomialkoeffisentene for 6 mynter og antall kron blir
1 6 15 20 15 6 1
De tilsvarende sannsynlighetene for å få disse utfallene, for myntkast er p=0.5, q=1-p=0.5
0.015625 0.093750 0.234375 0.312500 0.234375 0.093750 0.015625
Sannsynligheten for å få for eksempel 4 kron i 6 kast er ca. 23%
Summen av disse sannsynlighetene er lik 1.
Vi kan simuler myntkast ved å kaste en mynt 6 ganger, telle antall kron, og gjenta dette 10000 ganger.
Deretter plotter vi en tilsvarende normalfordeling med samme standardavvik og gjennomsnitt.
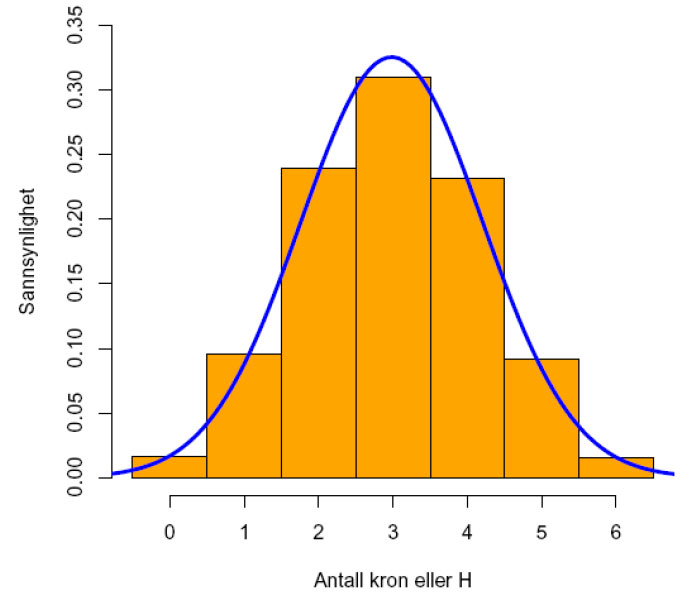
Simulering av 6 myntkast og sannsynlighten for utfallet kron eller bevege seg til høyre (H) når en ert treffer en pinne på et Galton-brett med 6 rader med pinner og 6 brønner på bunnen av brettet.
I en binomial fordeling er sannsynligheten for suksess k ganger i n uavhengige forsøk P(X=k) lik:
\(P(X=k)= \frac{n!}{k!(n-k)!} p^k q^{n-k}\;\;\;\;\;\; k=0, 1, 2, 3, .\dots,n\)
q er sannsynligheten for ikke-suksess.
Det vil si at kastes n antall mynter med p=0.5 så angir binomialfordelingen sannsynligheten for k kron i n-kast for hvert av heltallene av k mellom 0 og n.
Summen av alle punktsannsynlighetene, det vil si fordelingsfunksjonen F(x), er den kumulative sannsynligheten, og den blir alltid lik 1:
\(F(x)=\displaystyle\sum_{k=0}^n P(X=k)=\sum_{k=0}^n \frac{n!}{k!(n-k)!} p^k q^{n-k}=\sum_{k=0}^n \binom{n}{k} p^k q^{n-k}=(p+q)^n=1\)
For eksempel er P(a≤x≤b) gitt ved
\(F(x)\displaystyle\sum_{k=a}^b \binom{n}{k}p^k q^{n-k}\)
Forventningsverdien E(X) og varians Var(X) for en binomial fordeling er:
\(E(x)= np \;\;\;\;\; Var(x)=npq\)
For eksempel kast av 6 mynter er forventingen for antall kronE(x)=6·0.5 =3, varians Var(x)=1.5, standardavvik SD=1.
Oppgave
Lag et Galton-brett med trepinner. Kjøp tørre runde erter på butikken.

Et ikke optimalt konstruert Galton-brett. Det ble borret for mange rekker med hull. Trepinner er greit hvis man bruker erter, men med klinkekuler som er tyngre gikk det dårlig med trepinner, de gir rekyl på klinkekulene. Verktøy: drill, trepinner, treplate, noen lister til kanter, lim på kammere nederst. Dere klarer sikkert bedre enn det vi fikk til.