\(\displaystyle \sinh(x)=\frac{e^x - e^{-x}}{2}\;\;\;\;\;\cosh(x)=\frac{e^x + e^{-x}}{2}\;\;\;\;\;\tanh(x)=\frac{\sinh(x)}{\cosh(x)}\)
Hyperbolsk cosecant (csch(x)), hyperbolsk secant (sech(x)) og hyperbolsk kotangens (coth(x))
\(\displaystyle \text{csch(x)}=\frac{1}{\sinh(x)}\;\;\;\;\; \text{sech(x)}=\frac{1}{\sinh(x)}\;\;\;\;\; \text{coth(x)}=\frac{1}{\tan(x)}\)
Vi har også:
\(\cosh(0)= 1\;\;\;\, \sinh(0)= 0\;\;\;\;\cosh(-x)= \cosh(x)\;\;\;\; \sinh(-x)=\sinh(x)\)
\(\cosh x+\sinh x= e^x\;\;\;\;\cosh x-\sinh x= e^{-x}\;\;\;\; \cosh^2x -\sinh^2 x=1 \)
Vi har også inverse hyperbolske funksjoner sinh-1 og tanh-1.
\(\displaystyle y= \sinh^{-1}x \;\iff\;\; x= \sinh y\)
Siden hyperbolske funksjoner kan uttrykkes som eksponentialfunksjoner kan inverse hyperbolske funksjoner uttrykkes som logaritmer:
\(\displaystyle \sinh^{-1}x= \ln \left(x + \sqrt{x^2 + 1}\right)\)

Hyperbolsk sinus (sinh(x), sinus hyperbolicus).
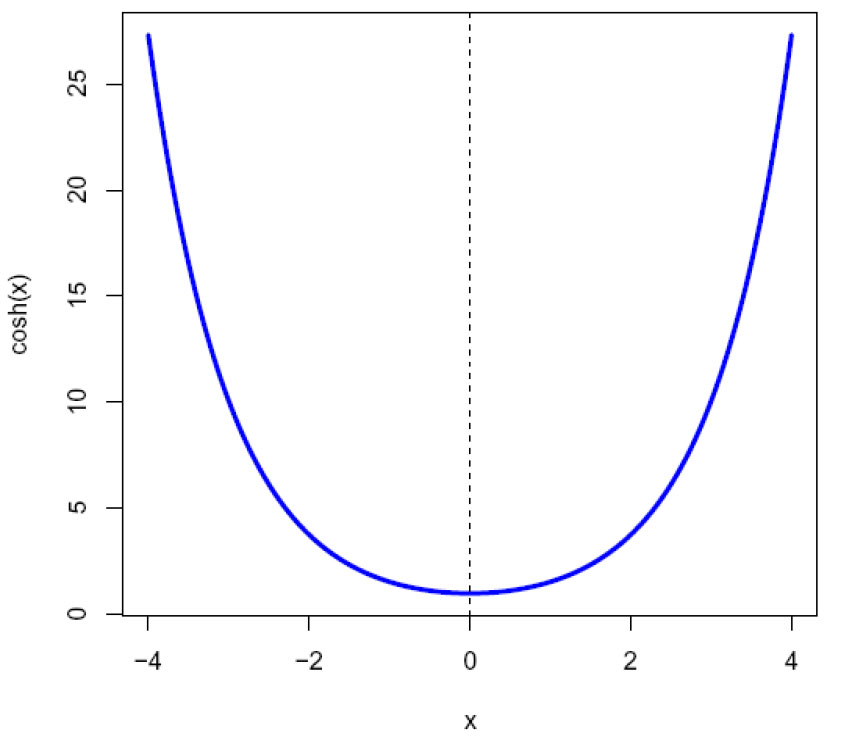
Hyperbolsk cosinus (cosh(x), cosinus hyperbolicus).
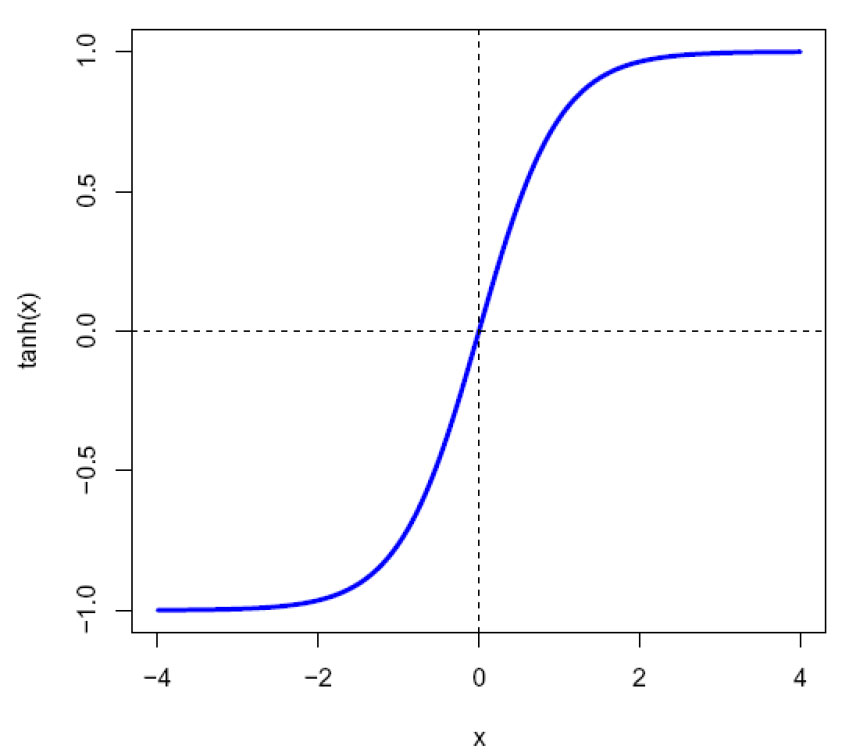
Hyperbolsk tangens (tanh(x), tangens hyperbolicus)

Hyperbolske funksjoner ble undersøkt av Leonard Euler og seinere av den italienske matematikeren Vincenzo Riccati (1707-1775). Det var den tyske matematikeren Johann Heinrich Lambert (1728-1777) som ga funksjonene navn, slik de er en del av hyperbolsk geometri. Lambert er også kjent for kartprojeksjoner.
Hvilken kurveform har en kjetting som henger fritt ned fra to stolper ?
Kurven kalt katenari (l. catena - kjede, catenaria, kataraktkurve, katenakjede, catenakjede) er en kjedekurve ble studert av Johann Bernoulli, Gottfried Leibniz og Christiaan Huygens, publisert i 1691 i Acta Eruditorum ,, og de kunne vise at kurveformen ikke var en parabel slik som Galileo Gelilei trodde. Robert Hook brukte dem til å konstruere buer i gjenoppbyggingen av St Paulskatedralen. En kjedekurve er et kjede eller en kabel som henger fritt ned fra to festepunkter, påvirket bare av gravitasjonskreftene (vekten av kjedet) og streknigskreftene (tensjonen) langs kjedet eller kabelen. Eksempler er kjettinger som skal markere overgang til en gressplen, telefonledninger mellom telefonstolper, kraftledninger som henger mellom kraftmaster eller strømlinjene for jernbane.. Ankerkjetting til en båt. I edderkoppspinn fra hjulspinnere henger de tverrgående trådene som katenarier.
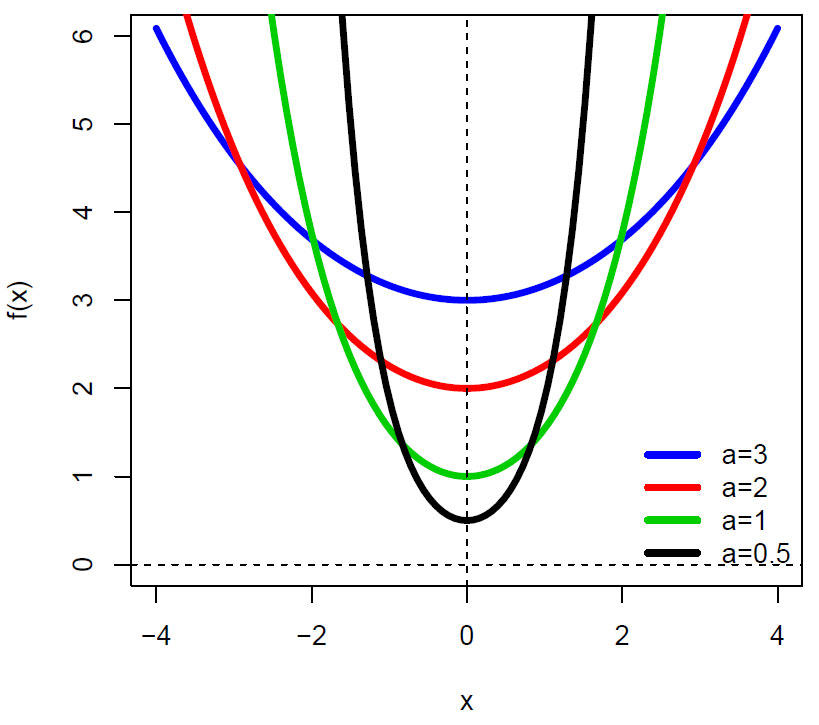
Matematisk er en kjedekurve beskrevet av en hyperbolsk kosinusfunksjon
\(\displaystyle y= a \cosh\left(\frac{x}{a}\right)\)
Figuren viser kjedekurven for forskjellige verdier av a.
Imidlertid blir kablene på en hengebru en parabel når de er festet til brokaret, men en catenaria når de henger fritt.
Funicular (velarkurve, seilkurve) er kurveformen på et firkantet seil i vind som henger mellom to horisontale stenger. Denne kurveformen ble undersøkt av Jacques Bernoulli.
Katenoide
En katenoide er det tredimensjonale resultatet av rotering av en katenarkurve omkring en akse.
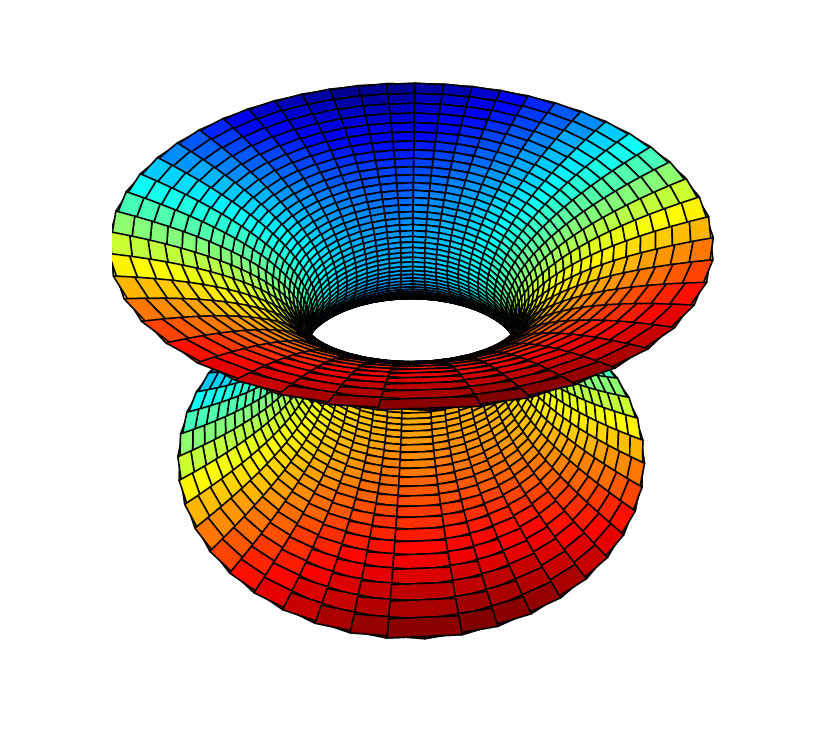
Katenoide med koordinatene nedenfor og a=8.
\(\displaystyle x= a\cosh \frac{\phi}{a} \cos \theta\)
\(\displaystyle y= a\cosh \frac{\phi}{a} \sin \theta\)
\(\displaystyle z= \phi\)
Litteratur
Apostol, T.M. Calculus (Vol I + II). Blaisdell Publ. Comp. 1962.
R Development Core Team (2011). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0, URL http://www.R-project.org/.
Wikipedia