Vi ønsker å ha tall som gir svar i alle ligninger. Har vi ligningen:
\(x^2 + 1=0\;\;\;\;\;\implies \; x=\sqrt{-1}\)
Vi kan ikke ta kvadratrot av et negativt tall. Dette førte fram til de komplekse tall, for at tallrekken skal være komplett.
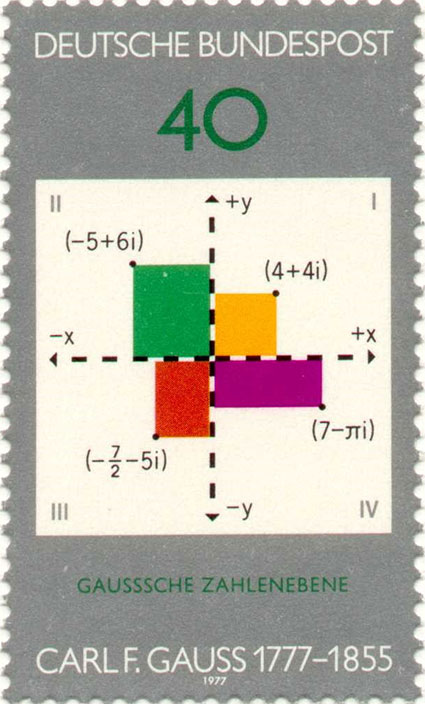
Kompleksplanet kalles gaussplan, argandplan eller wesselplan
For det komplekse tallet:
\(z= 2 + 3i\)
så er det 2 på den reelle aksen og 3 på den imaginære aksen. Vi kan finne modulus til et komplekst tall, det vil si avstanden (r) fra origo til koordinatene (a,b) i et komplekst tall z=a+bi, i vårt eksempel (2,3). Argumentet til det komplekse tallet er vinkelen mellom reell akse og vektoren som går fra origo (0,0) til (a,b), regnet mot klokka. Det komplekse tallet kan roteres inntil 2π (0, 2π), og i multipler av 2π, men det er vanlig å bruke intervallet (-π, π). Det komplekse tallet 0 (0+ 0i) har modulus lik 0.
Vi kan plotte det imaginære tallet med en reell akse (Re(z)) og imaginær akse (Im(z))
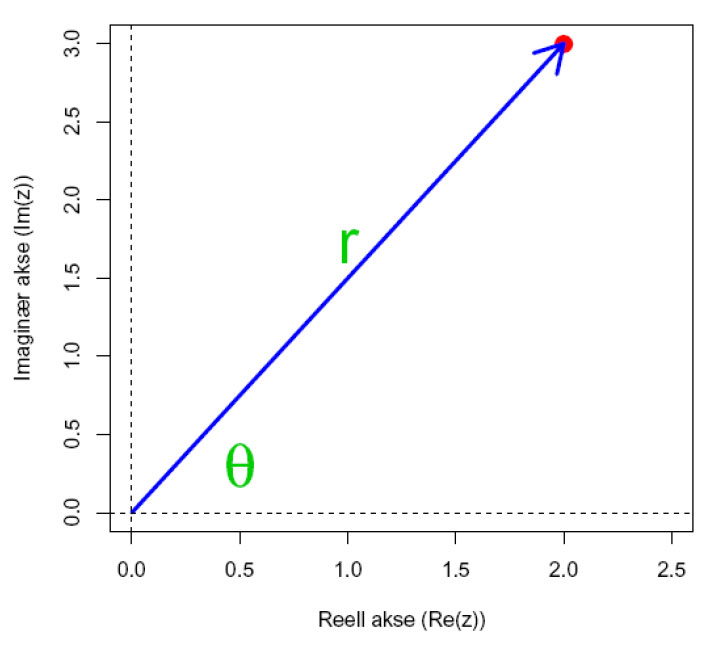
Det komplekse tallet z = 2 + 3i. Den greske bokstaven theta (θ) angir vinkelen, modulus z = 3.605551, og argument z er lik 0.9827937.
Lengden av z lik modulus z (|z|) blir ifølge Pythagoras hvor a og b er kateter og r=|z| er hypotenus:
\(|z|=r=\sqrt{a^2 + b^2}\)
Komplekse tall kan uttrykkes i form av enhetskoordinatvektorene (1,0) og (0,1) slik at
(a,b) = (a,0) + b(0,1)
En vektor har lengde og retning, og i det komplekse plan har det komplekse tallet z det ordnete paret (a,b). Ethvert komplekst tall kan uttrykkes som et ordnet par. De komplekse tallene er en utvidelse av de relle tallene som bare har en reell del.
Vi har et komplekst tall z, hvor vi bytter ut (a,b) med (x,y):
\(z=x + yi\)
Et komplekst tall kan ha en polar representasjon, hvor koordinatpunktet (x,y) erstattes med radius r og vinktel theta (r,θ). Vi kan uttrykke (x,y) som polarkoordinater:
\(x= r \cos \theta\;\;\;\;\; y = r \sin \theta\;\;\;\;\; -\pi<\theta<\pi\)
Vi kan da skrive:
\(z=x+yi=r(\cos \theta + i \sin \theta)=re^{i \theta}\)
hvor r er lik lengden (modulus) til z og vinkelen theta (θ) er argumentet til z.
Det betyr at et komplekst tall med modulus=1, |z|=1
får retningsfaktoren:
\(\cos \theta + i \sin \theta \)
siden:
\(\cos ^2 \theta+ \sin ^2 \theta=1\)
Lengden (modulus) eller absoluttverdi |z| = r som er avstanden (x,y) til origo (0 + 0i) er:
\(mod|x+yi|=r=|x+yi|=\sqrt{x^2 + y^2}\)
og polarvinkelen θ (mot klokka) kalles argument til x+yi (arg z).
\(arg(z)= arg|x+yi|=\theta\)
Den komplekse funksjonen:
\(z(\theta) = re^{i\theta}\)
blir en sirkel med radius r
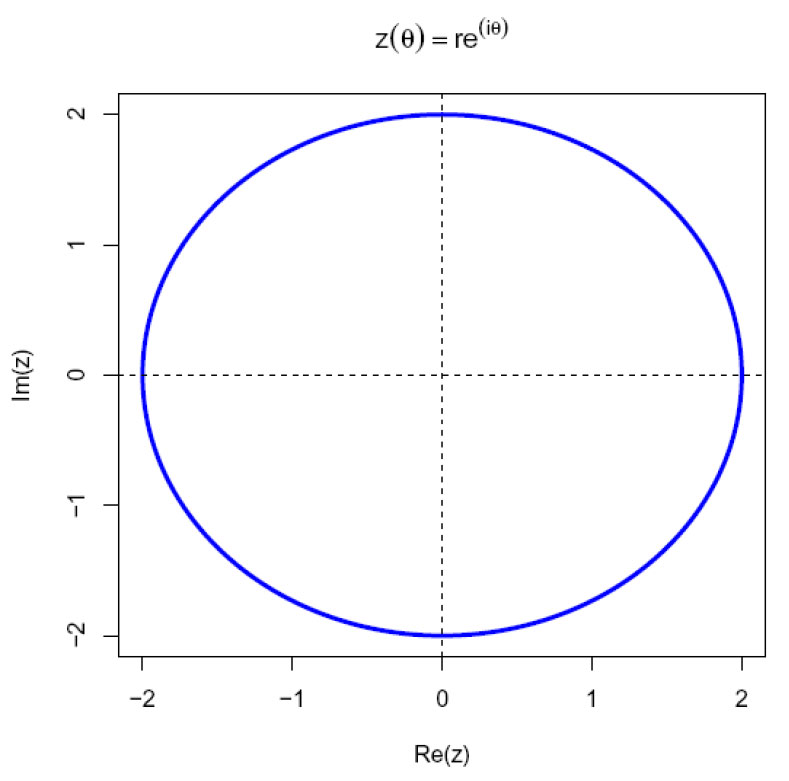
Vinkel 2π-radianer og radius = 2
Vi benytter Eulers formel som viser sammenhengen mellom trigonometriske funksjoner og den komplekse eksponentialfunksjonen, hvor e er basis i naturlige logaritmer:
\(e^{i\theta}=\cos \theta + i\sin \theta\)
gir dette at z kan også skrives som polar presentasjon:
\(z=re^{i \theta}\)
Vi har også:
\(|e^{i\theta}|=\sqrt{\cos^2 \theta+\sin^2 \theta}=1\)
Euler fant sammenhengen som kobler sammen pi (π), det naturlige tallet e og det imaginære i:
\(e^{i \pi}+1=0\)
Hvis vi har et komplekst tall z=x+yi så vil det komplekse konjugatet
\(\overline z= x-yi\)
være speiling av z omkring x-aksen:
\(z\overline z=(x+yi)(x-yi)= x^2 + y^2=|z|^2\)
Multipliserer vi et komplekst tall z=a+bi med det komplekse konjugatet hvor fortegnet på i snus, så får vi et reelt tall:
\(z\overline z= a^2 + b^2 \;\;\;\; \text{hvor} \;\;\overline z=a-bi\)
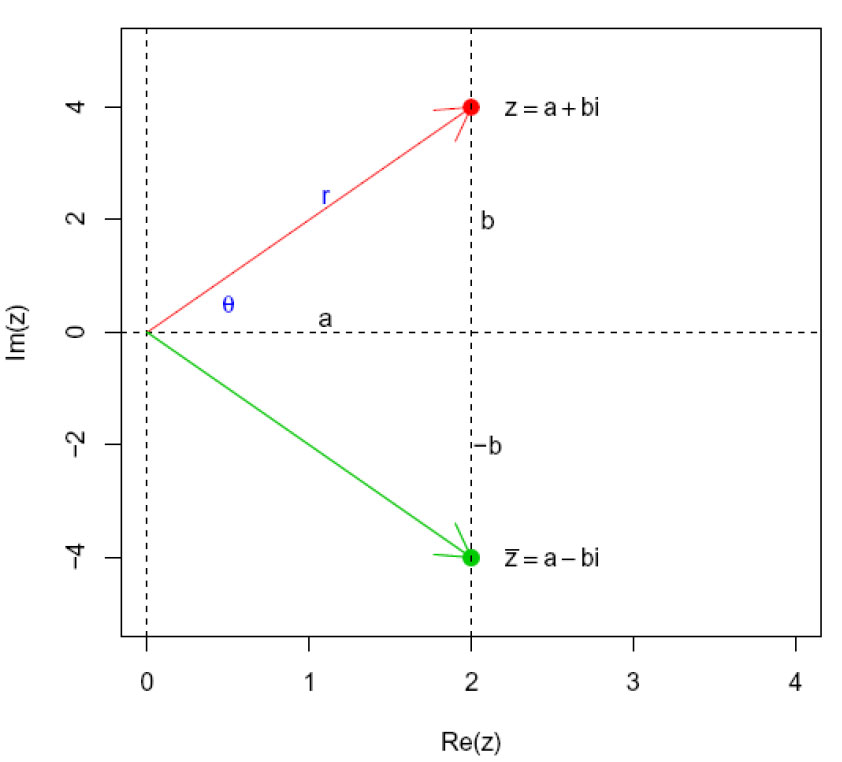
Komplekst tall z = 2 + 4i og komplekst konjugat
Når vi betrakter komplekse tall som ordnete par (x1,x2) så kan vi addere og multiplisere på samme måte som for todimensjonale vektorer:
\((x_1, x_2) + (y_1,y_2)= (x_1 + y_1, x_2 + y_2))\)
\(a \cdot (x_1, x_2)= (ax_1, ax_2)\)
\((x_1,x_2)\cdot (y_1, y_2)= (x_1 y_1- x_2y_2, x_1y_2+x_2y_1)\)
\(\displaystyle\frac{1}{(x_1, x_2)}=\left(\frac{x_1}{x_1^2+x_2^2}, \frac{-x_2}{x_1^2+x_2^2}\right)\;\;\;\;\;\; (x_1, x_2) \neq (0,0)\)
Nullkomplekstallet er lik (0,0).
De komplekse tallene er en utvidelse av de reelle tallene som bare har en reell del. Vi kan summere komplekse tall:
\((a+bi) + (c + di)= (a+ c)+ (b+d)i\)
Multiplisere komplekse tall:
\((a+bi) \cdot(c+ di)=(ac-bd)+(bc+ad)i\)
Komplekse tall kan brukes i de fleste funksjoner.
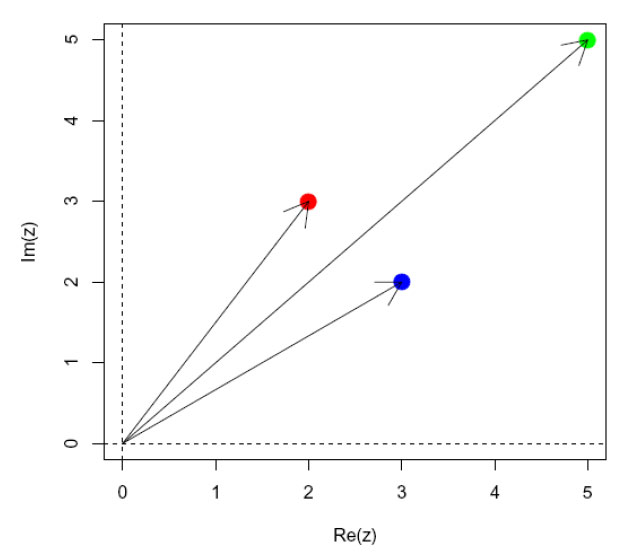
Summering av to komplekse tall. Summen av de to komplekse tallene z1 = 2 + 3i og z2 = 3 + 2i. z1 + z2 = z3, hvor z3= 5 + 5i . Re(z) er reell akse og Im(z) er imaginær akse. Origo er (0 + 0i). Summen av de komplekse tallene er diagonalen i et parallellogram med kanter dannet av de to komplekse tallene. Et parallellogram består av to kongruente trekanter.
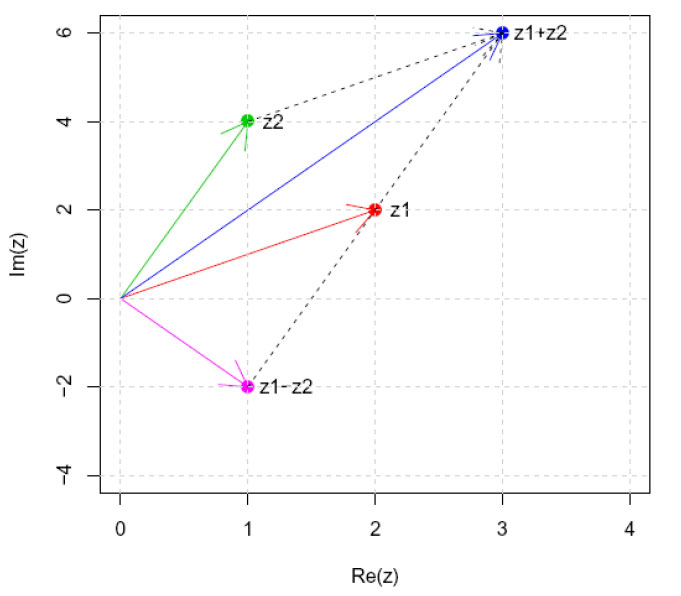
To komplekse tall z1= 2 + 2i og z2 = 1 + 4i, summen av dem z1+z2 = 3 + 6i, og substraksjon z1-z2 = 1-2i.
Multiplikasjon og divisjon av komplekse tall
Vi kan multiplisere to komplekse tall hvor vi erstatter i2 med -1.
\((a+bi)^2= (a+bi)(a+bi)= (a^2 - b^2)+(2ab)i\)
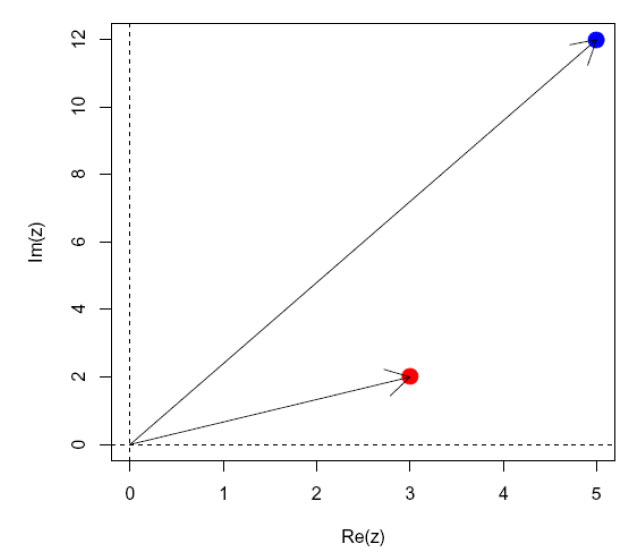
Multiplisering av det komplekse tallet z = 3+2i med seg selv og produktet z2. Multiplikasjon av et komplekst tall med seg selv dobler vinkelen og kvadrerer avstanden fra origo.
Multiplisering av komplekse tall, husk at i2 = -1
\((a+bi)(c+di)= (ac-bd)+(bc+ad)i\)
\((2+3i)(4+5i)=(8-15)(12+10)i=-7+22i\)
Multiplisering av to komplekse tall vil si å multiplisere moduli og summere polarvinklene.
Vi kan skrive opp de komplekse tallene z og w i polar representasjon:
\(z=r_1(\cos \theta+ i\sin \theta)\;\;\;\;\;\; w=r_2(\cos \phi + i\sin \phi)\)
\(z\cdot w= r_1r_2\left[(\cos \theta\cos \phi-\sin \theta\sin \phi)+(\cos \theta\sin\phi+\cos\phi \sin\theta)i\right]= r_1r_2\left[\cos(\theta+\phi)+\sin(\theta+\phi) \right]\)
Vi kan finne den resiproke til et komplekstall (≠0):
\(\displaystyle\frac{1}{a+bi}=\frac{a-bi}{(a+bi)(a-bi)}=\frac{a-bi}{a^2 + b^2}= \frac{a}{a^2 + b^2}-\frac{bi}{a^2 + b^2}\)
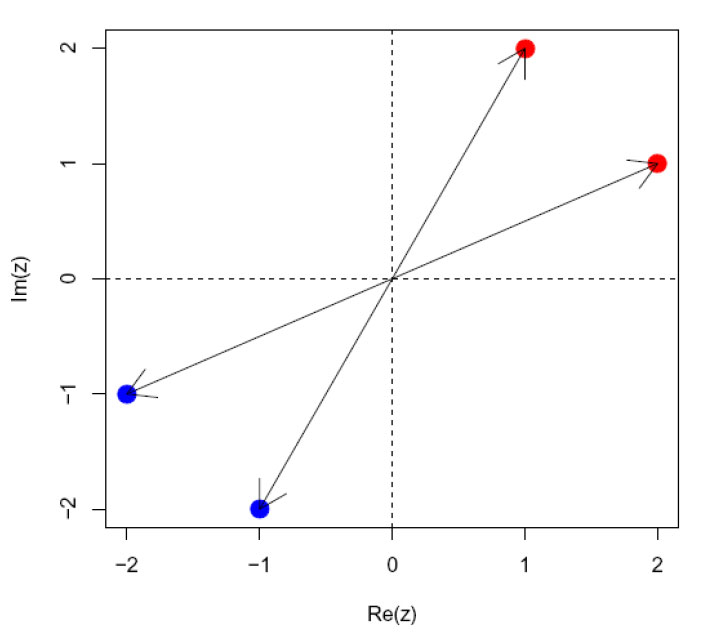
To komplekse tall rotert 180 grader (180o).
Hvis vi har det komplekse tallet z = x + yi så har vi det komplekse konjugatet:
\(\overline z= x-iy\)
Hvis man har et komplekst tall z = 2 + i så blir det komplekse konjugatet lik 2 – i.
Multiplikasjon av et komplekst tall z med det komplekse konjugatet til z gir et reelt tall ≥0
\(z\cdot \overline z=|z|^2= (a^2 + b^2)\)
Hvis man har et komplekst tall z = 2 + i så blir det komplekse konjugatet lik 2 – i.
Multiplikasjon av et komplekst tall z med det komplekse konjugatet til z gir et reelt tall ≥0
\(\displaystyle\frac{z_1}{z_2}\cdot \frac{\overline z_2}{\overline z_2}=\frac{z_1\overline z_2}{z_2\overline z_2}=\frac{z_1\overline z_2}{|z_2|^2}\)
Vi kan gjøre tilsvarende multiplikasjon og divisjon, men nå som polarkoordinater:
\(z_1=|z_1|e^{i\theta_1}\;\;\;\;\;\; z_2= |z_2|e^{i\theta_2}\)
Vi benytter nå eksponentialloven som også gjelder for komplekse tall:
\(z_1\cdot z_2=|z_1|\cdot|z_2|e^{i(\theta_1+\theta_2)}\)
For divisjon bruker vi de Moivres formel:
\(z=|z|(\cos \theta+i\sin \theta)= |z|e^{i\theta}\)
Det komplekse konjugatet:
\(\overline z= |z|(\cos \theta -i\sin \theta)=|z|e^{-i\theta}\)
\(\displaystyle\frac{1}{z}=\frac{\overline z}{z\overline z}=\frac{e^{-i\theta}}{|z|}\)
\(\displaystyle\frac{z_1}{z_2}=\frac{|z_1|}{|z_2|}e^{i(\theta_1-\theta_2)}\)

Komplekse tall z1= 2 + 2i og z2 = 1 + 4i, produktet z1·z2 = -6 + 10i og divisjonen z1/z2 = 0.59 -0.36i.
For to komplekse tall z og w:
\(\frac{w}{z}= \frac{w\cdot \overline z}{z \cdot \overline z}=\frac{w \cdot \overline z}{|z|^2}\;\;\;\;\;\; z\neq 0\)
kvadratroten av komplekse tall
Hvis vi har et komplekst tall
\(z= x + yi \;\;\;\;\; z= r(\cos \theta + (\sin \theta)i)\)
så blir kvadratet lik:
\(z^2 = (x + yi)(x+yi)= x^2 - y^2+ (2xy)i\)
\(z^2 = r^2 (\cos 2\theta + (\sin 2\theta)i) \)
det vil si kvadrering av modulus og dobling av polarvinkelen.
Kvadratroten av z i form av polarvinkler blir:
\(\sqrt{z}= \pm \sqrt{r}\left(\cos \frac{\theta}{2}+(\sin \frac{\theta}{2})i\right)\)
som er det samme som kvadratroten av modulus og halvering av polarvinkelen, og den andre kvadratroten blir det negative av dette.
Vi kan finne n-te roten av et komplekst tall slik at:
\(w^n= z\)
Hvis vi har wn=1 så gjelder:
\(w_n= |z|^{\frac{1}{2}}\left(\cos \left(\frac{2(n-1)\pi}{n}\right)+i\sin\left(\frac{\theta + 2\pi}{n}\right)\right)\)
og alle røttene blir liggende på en sirkel med sentrum i origo og radius |z|1/n.
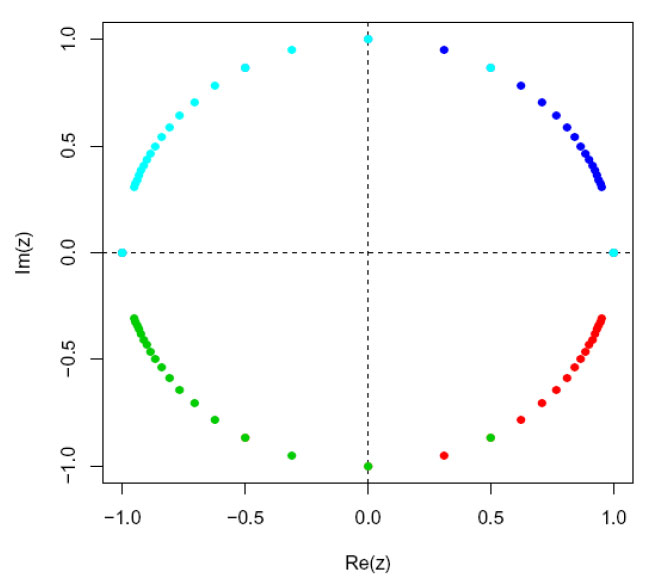
n-te roten blir liggende på en sirkel med radius 1.
Inverst komplekst tall
Det finnes bare et inverst kompleks tall z-1 til z slik at
\(z \cdot z^{-1}=1\;\;\;\;\; z^{-1}= \frac{1}{z}\;\;\;\;\; z\neq0\)
Det betyr også at:
\(\arg z^{-1}= -\arg z\)
og at:
\(\mod z^{-1}= \frac{1}{\mod z}\)
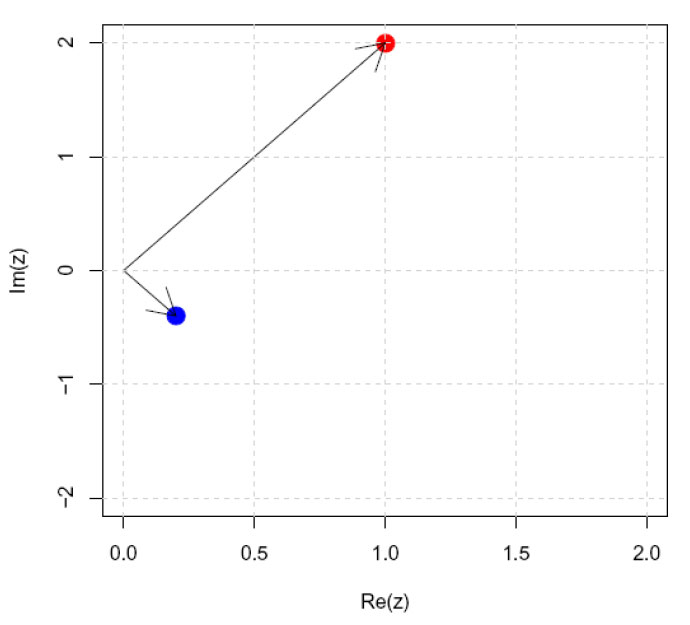
Komplekst tall z= 1+ 2i og det inverse 1/z= 0.2 – 0.4i
Eksponentialfunksjonen for komplekse tall
Eksponentialfunksjonen for komplekse tall må kunne følge samme regneregler som for reelle tall, e.g. for de komplekse tallene z1 og z2:
\(e^{z1}\cdot e^{z_2}= e^{z_1 + z_2}\)
og vi må kunne skrive:
\(e^{x+yi}= e^x \cdot e^{yi}\)
Hvis z=x+iy så vil ez være et komplekst tall:
\(e^z= e^x \left(\cos y + i\sin y\right)\)
Hvis vi har vinkelen θ så har vi:
\(e^{i\theta}=\cos \theta + i\sin \theta\)

Det betyr at komplekse tall kan uttrykkes som kompleks eksponentialfunksjon. Et komplekst tall z med modulus (absoluttlengde) r = |z| og med vinkel (argument) θ kan da skrives som:
\(z=x + yi= re^{i\theta}\;\;\;\;\; r=|x+yi |\;\;\;\;\theta = \arg (x+yi) + 2n\pi\)
Dette er en nyttig formel for multiplikasjon og divisjon av komplekse tall. Vi kan betrakte eiθ som et punkt på enhetssirkelen.
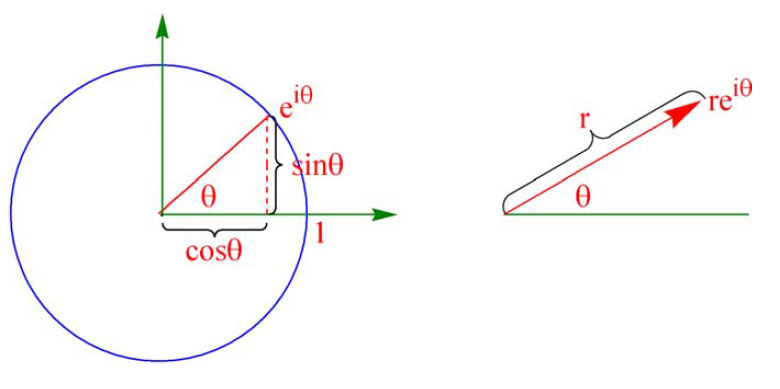
Hvis vi har to komplekse tall z1=r1eiθ og z2=r2eiφ så vil:
\(z_1z_2=r_1e^{i\theta} \cdot r_2e^{\phi}= r_1 r_2 e^{i(\theta + \phi)}\)
\(\displaystyle\frac{z_1}{z_2}=\frac{r_1 e^{i\theta}}{r_2 e^{i\phi}}= \frac{r_1}{r_2}e^{i(\theta + \phi)}\)
For eksempel det komplekse tallet z = (1,1) = 1+i med argument lik π/4 og modulus lik
\(\sqrt{2}= 1.414214 \dots\)
\(|z|=r=|1+1i|= \sqrt{1^2 + 1^2}\)
og kan skrives som:
\(z= \sqrt{2}\;e^{\frac{i\pi}{4}}\)
Euler kunne vise at:
\(1=\cos ^2 \theta + \sin ^2 \theta=(\cos \theta +i \sin \theta)(cos \theta - i\sin \theta)\)
og fant videre den interessante sammenhengen mellom det naturlige tallet e, π og i ved:
\(e^{i\pi}=\cos \pi + i\sin \pi\)
Euler gjorde det derved mulig å løse ligningen ex = -1 hvor svaret er
x =iπ. Det betyr at eiπ = -1
\(e^{i\pi}=\cos \pi + i\sin \pi= -1 + i\cdot 0=-1\)

\(\displaystyle e^{\frac{i\pi}{2}}= i\;\;\;\; \;e^{i\pi}=-1\;\;\;\;\;e^{\frac{3i\pi}{2}}= -i\;\;\;\;\;e^{i2\pi}=1\)
\(\ln(-1)= i\pi\;\;\;\;\;\; \ln (\pm i)= \pm \frac{1}{2}\pi i\)
\(e^{i \pi}=\cos \theta + i \sin \theta\;\;\;\;\; \text{Eulers ligning}\)
\(\sin \theta= \frac{1}{2i}\left(e^{i \theta}- e^{-i\theta}\right)\;\;\;\;\;\; \cos \theta= \frac{1}{2}\left(e^{i \theta}+ e^{-i\theta}\right)\)
\(\sin (i\theta)= i\sinh \theta\;\;\;\;\;\cos (i\theta)= \cosh \theta\;\;\;\;\; \sinh(i\theta)=i \sin (\theta) \;\;\;\;\, \cosh (i\theta)= \cosh\theta\)
For det komplekse tallet z = a + bi så følger:
\(z^2=(a^2 - b^2 ) + 2abi\)
\(z^3= (a^3 - 3ab^2)+ (3a^2 b-b^3)i\)
Hvis vi har et komplekst tall og det komplekse konjugatet:
\(z= a + bi \;\;\;\;\; \overline z = a-bi\)
Så følger:
\(|z|^2 = z \cdot \overline z= a^2 + b^2\)
\(e^z = e^a \left(\cos b + i \sin b\right)\)
Komplekse logaritmer
Logartimefunksjonen og eksponentialfunksjonen er inverse funksjoner og gjelder også for komplekse tall:
\(e^{\ln z}= z= |z|e^{i\theta}= e^{\ln |z|}\;e^{i\theta}= e^{\ln |z| + i\theta}\)
Det betyr at:
\(\ln z=\ln |z|+ i\arg(z)\)
Den reelle delen blir den naturlige logaritmen til z, men i den imaginære delen inngår argumentet til z, som man må vite.
Litteratur:
Apostol, T.M. Calculus (Vol I + II). Blaisdell Publ. Comp. 1962.
R Development Core Team (2011). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0, URL http://www.R-project.org/.
Rottmann, Karl: Matematische Formelsammlung. Bibliographisces Insitutt. Hochschultaschenbücher-Verlag. 1960.
Wikipedia