
Pilkast på et dartbrett hvor koordinatene for treffpunktene (x,y) i de fire kvadrantene i et rettvinklet koordinatsystem med blinken i origo blir bestemt med en tommestokk. Fortegnet på koordinatene er avhengig av i hvilken kvadrant treffpunktet ligger.
Tallene angir kvadrantene 1-4 regnet mot klokka på en sirkelrund skive med origo for koordinatsystemet i sentrum av blinken.
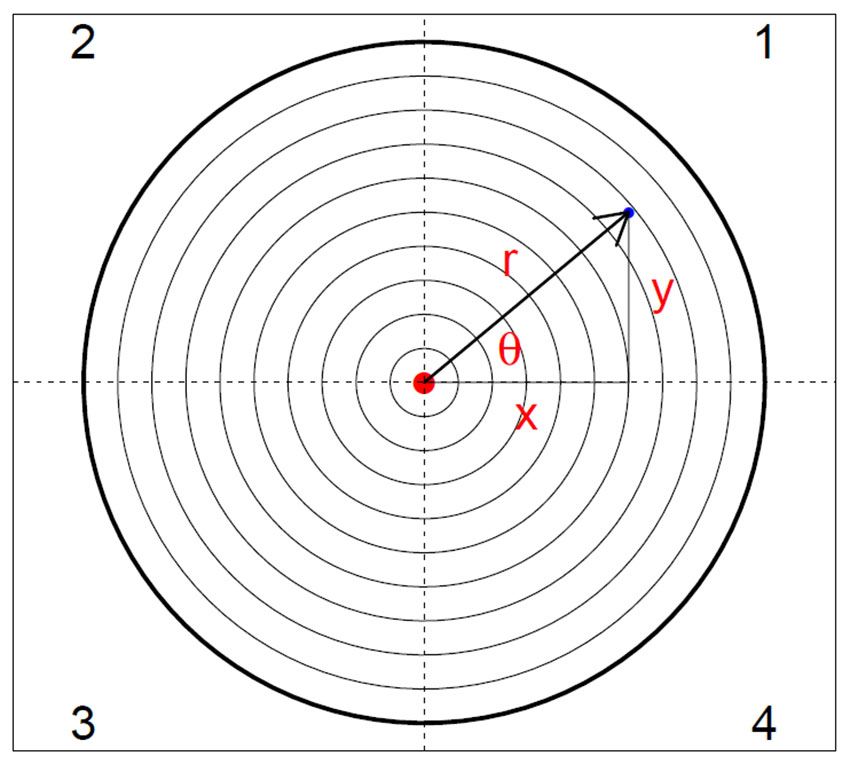
Fra koordinatene for treffpunktene (x, y) for pilkast kan man kan lage et estimat av π, og finne koblinger til de sannsynlighetsfordelingene normalfordeling, standard normalfordeling, kjikvadrat (χ2)- fordeling og Rayleighfordeling. Nedenfor er dette vist som en simulering og et praktisk eksperiment. Det er 360o i en sirkel tilsvarende 2π radianer. Hvis en sirkel har radius r og fasevinkel θ så vil lengden (L)av den tilsvarende buen på sirkelen avgrenset av de to vinkelbeina være θ=L/r. Hvis fasevinkelen θ=360o, det vil si gå rundt hele omkretsen på sirkelen 2πr. Med radius r=1 har man enhetssirkelen.
\(\theta=\frac{2\pi r}{r}=2\pi \: \; radianer\)
Simulering av pilkast
Simulerer normalfordelte kast av dartpiler mot en blink hvor treffpunktene er angitt med koordinatene (x, y), x og y er uavhengige av hverandre og standard normalfordelte med lik varians, standardavvik lik en, og gjennomsnitt lik null. Fasevinkel er theta (θ) og radius r > 0.
Kvadratet av avstanden (r2) fra blinken følger Pythagoras setning:
\(x^2 + y^2 = r^2 \; \; \; \; \;\; r = \sqrt{x^2 +y^2 }\)
For cosinus og sinus til fasevinkel, samt fasevinkel theta (θ) lik invers tangens (arctan)
\(cos \theta= \frac{x}{r} \; \; \; \; sin\theta= \frac{y}{r} \; \; \; \; \theta=arctan \frac{y}{x}\)
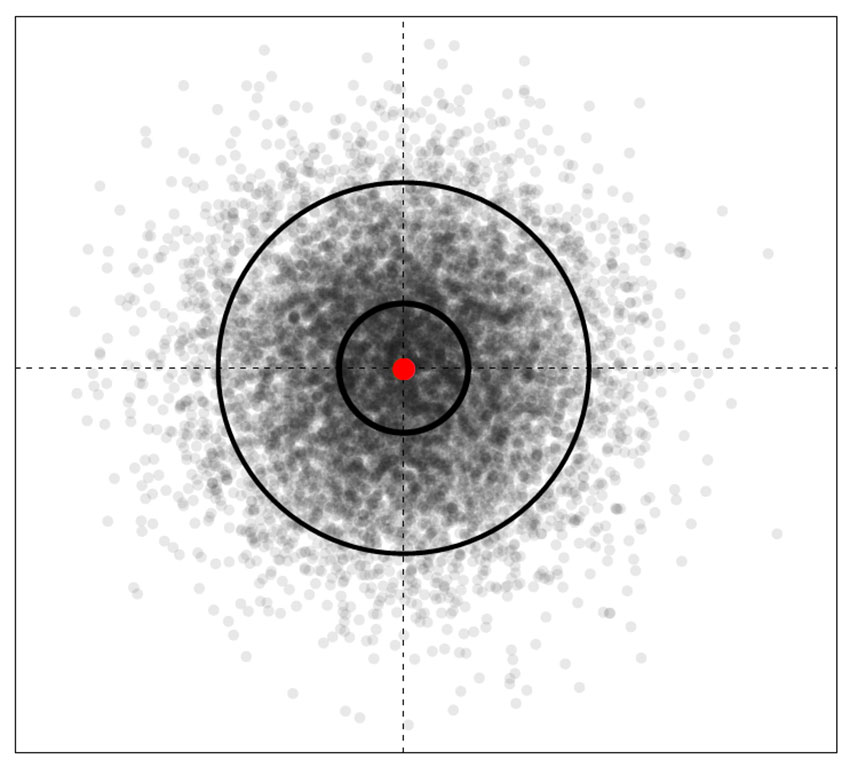
Simulert pilkast med 10000 treffpunkter med pseudoslumptall for standard normalfordelte x og y. Den innerste sirkel angir 1 standardavvik og den ytterste 1.96·standardavvik. Simuleringen utført i statistikk og programmeringsspråket R.
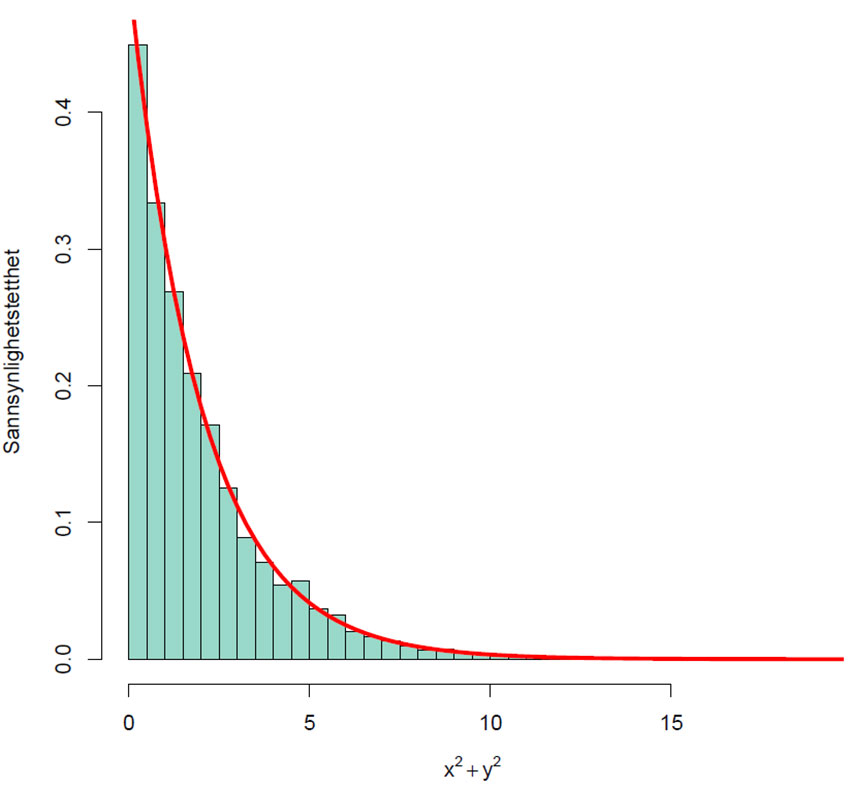
Histogram for fordelingen av kvadrert radius r2 for 10000 simulerte treffpunkter. Heltrukken rød linje viser kjikvadratfordelingen med to frihetsgrader. Kvadratsummer følger kjikvadratfordelingen (χ2) hvor antall frihetsgrader (df) er lik antall uavhengige standard normalfordelte variable, i dette tilfelle blir df=2. Kjikvadratfordelingen (CHI) er et spesialtilfelle av gammafordelingen (GAMMA), og med df=2 følger den også eksponentialfordelingen (EXP). X ~CHI(2) = EXP(2) = GAMMA(1,1/2). Disse to sistnevnt ville også ha fulgt den røde linjen. Fasevinkelen theta (θ) vil følge en uniform fordeling.
Rayleighfordelingen
Rayleighfordelingen er kontinuerlig og beskriver fordelingen av en retningsavhengig vektor med to uavhengige koordinater, her x og y. Den vil også beskrive absoluttverdien til komplekse tall. Rayleighfordelingen og Ricefordelingen er involvert i lineære tidsvariantsystemer.
Sannsynlighetstettfordelingen f(x) av Rayleighfordelingen er:
\(f(x)=\frac{x}{\sigma^2}e^{-\frac{x^2}{2\sigma^2}}\)
Forventningen E(X) og varians Var(X) er lik:
\(E(X)=\sigma \sqrt{\frac{\pi}{2}}\; \; \; \; \; \; Var(X)=\frac{4-\pi}{2}\sigma^2\)
Fordelingen av radius (r) til treffpunktet kan beskrives av en Rayleighfordeling, i vårt eksempel er σ=1.
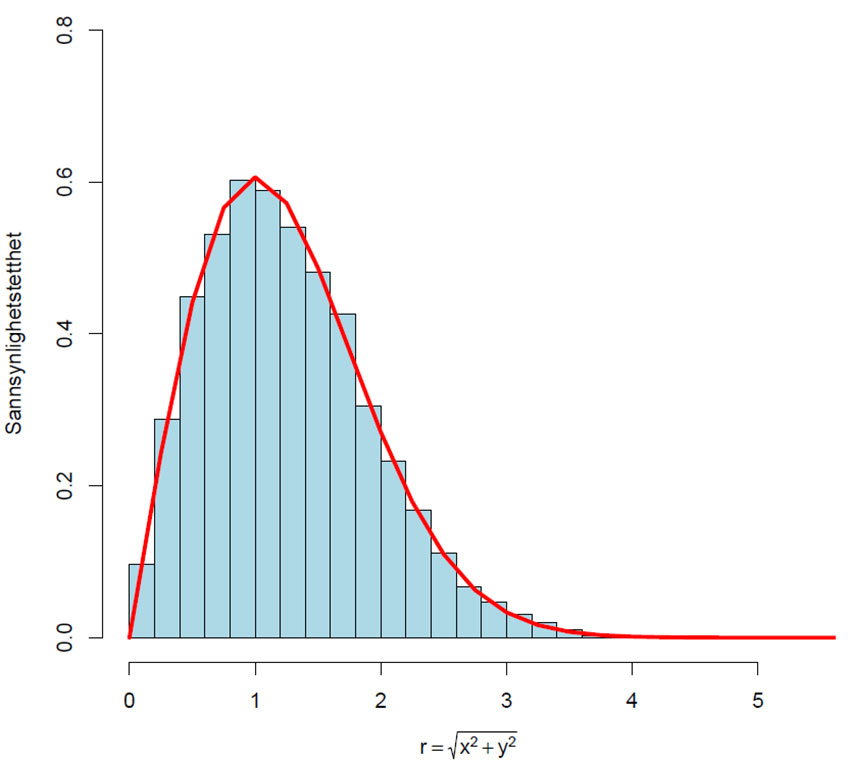
Histogrammet viser fordelingen av radius r for 10000 simulerte pilkast med x- og y-koordinater fra tilfeldige tall fra standard normalfordeling. Den heltrukne røde linjen viser sannsynlighetstetthetfunksjonen for Rayleighfordelingen. I denne ene simuleringen ble estimatet for π=3.17 og varians 0.429. Ved gjentatte simuleringer kan man lage et estimat av π med tilhørende 95% konfidensintervall.
Komplekse tall og pilkast
De komplekse tallene er en utvidelse av de relle tallene og kan fremstilles geometrisk i kompleksplanet med en horisontal reell x-akse (Re(z)) og en vertikal imaginær yi-akse (Im(z)). Euler innførte tallet i kalt imaginær enhet :
\(i=\sqrt{-1}\)
Vi har det komplekse tallet z:
\(z= x + yi\)
Lengden modulus (mod(z)) eller absoluttverdi |z|=r er avstanden (x,y) til origo, altså lik lengden av radius r.
\(mod\left|x + yi \right|=r=\left|x + yi \right|=\sqrt{x^2 + y^2}\)
og polarvinkelen θ (theta, mot klokka) kalt argument (arg(z)) til x+yi er
\(arg(z)= arg\left|x+yi\right|=\theta\)
For 10000 simulerte x- og y-koordinatene fra pseudorandome tall fra standard normalfordeling lar vi x representere henholdsvis reell akse (Re(z)) og y imaginær del av komplekse tall (Im(z)), og lager deretter en plot av treffpunktene i kompleksplanet.
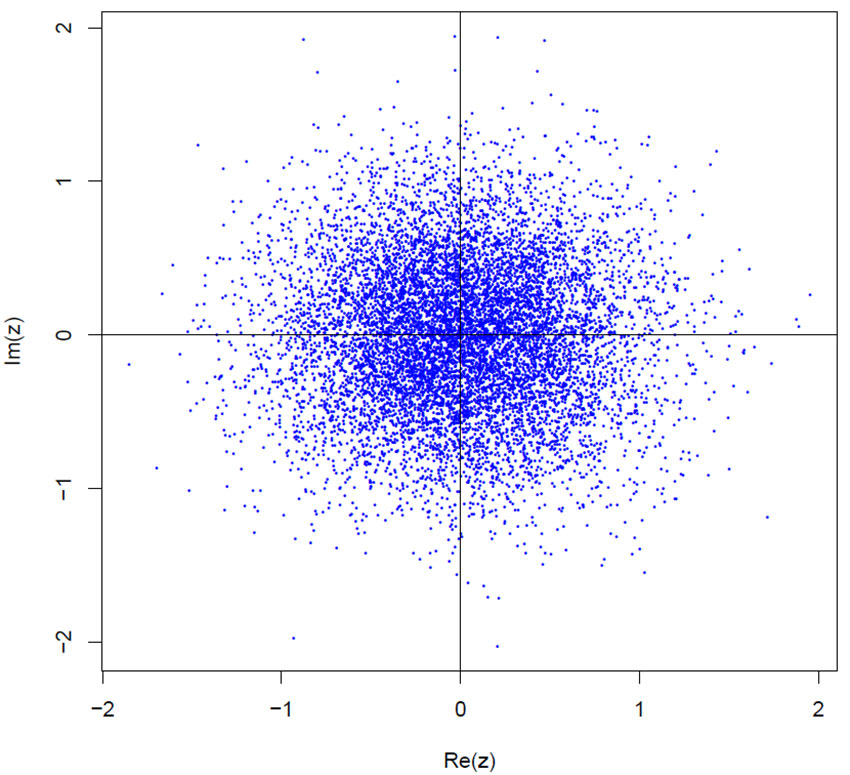
Simulerte treffpunkt for pilkast vist i kompleksplanet.
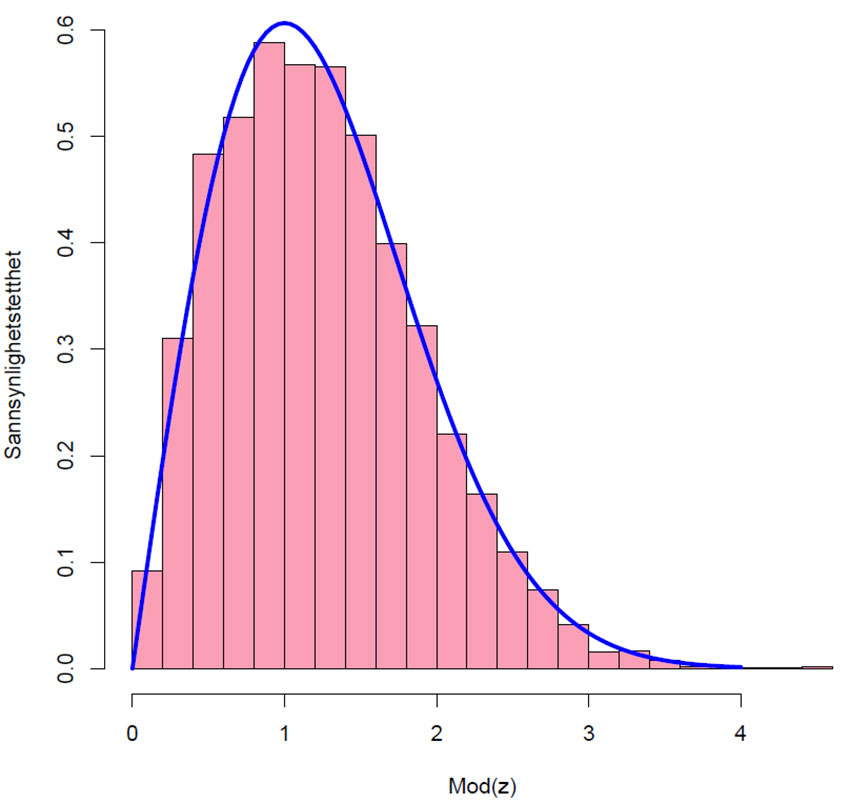
Figur som viser modulus z, altså fordeling av radius r, og vi ser at dette som tidligere følger Rayleighfordelingen (heltrukken blå linje).
Pilkast og Ricefordelingen
Ricefordelingen beskriver en tilfeldig bivariat normalfordeling for x og y, men hvor gjennomsnittet er forskjellig fra null. Vi kan snu dartbrettet til den andre siden, og ser at forskjellige seksjoner gir forskjellig poengutbytte, og hvor det ikke lenger gjelder å treffe ”okseøye”. Sentrum av fordelingen (a, b) er nå i avstand v fra origo.
\(v= \sqrt{\overline a^2 + \overline b^2}\)
Avstanden R fra origo til treffpunktene blir nå:
\(R=\sqrt{a^2 + b^2}\)
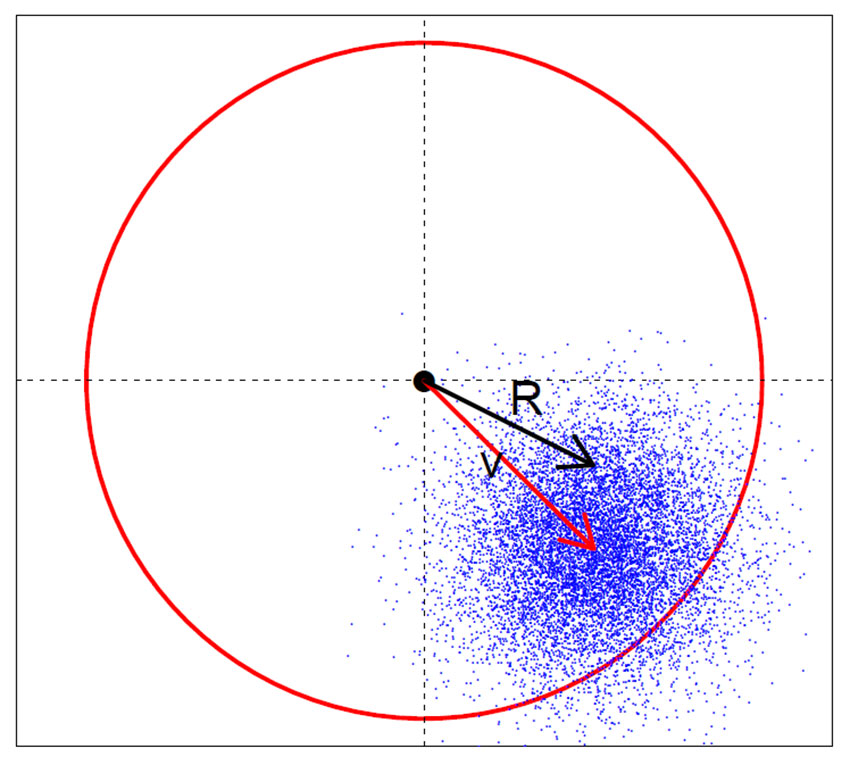
Simulerte pilkast (n=10000) med koordinater (a,b) fra en normalfordeling med gjennomsnitt henholdsvis 0.5 og -0.5 og standardavvik 0.2 for begge.
Praktisk labeksperiment pilkast
En modell og simulering er uten verdi hvis den ikke kan kobles til eksperimenter eller observasjonsstudier. I emnet BIO2150 Biostatistikk og studiedesign (siste gang 2018) var en av oppgavene praktisk pilkast. Hvert lag kaster 10 piler og bestemmer x-, y-koordinatene (cm) for treffpunktene med en tommestokk. Avstand 2 meter fra blinken. Origo midt i blinken med tilhørende ortogonalt aksesystem, med fortegn på x- og y-koordinatene i de forskjellige kvadrantene. I alt 12 forskjellige lag for hvert årskull 2015-2018 (pilkastH18.txt), med noen NA-verdier.
Er treffpunktene for x- og y-koordinatene normalfordelte ? Ja, det ser noenlunde sli ut.
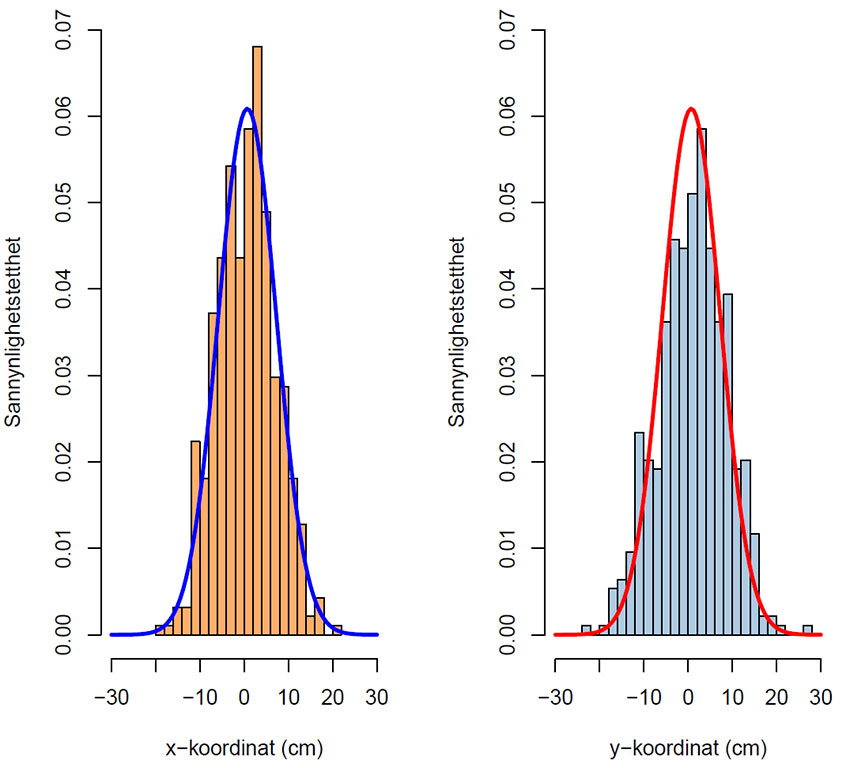
Histogram for x-koordinater og y-koordinater treffpunkt i pilkasteksperiment med en tilhørende normalfordeling som heltrukken linje.
Regner om til standard normalfordeling, og lager histogram for kvadratet av radien (r2) til treffpunktene:

Figur fra pilkasteksperiment som viser histogram for r2, samt heltrukken linje for sannsynlighetstettheten kjikvadratfordeling med to frihetsgrader. Det er rimelig godt samsvar mellom eksperiment og simulert modell.
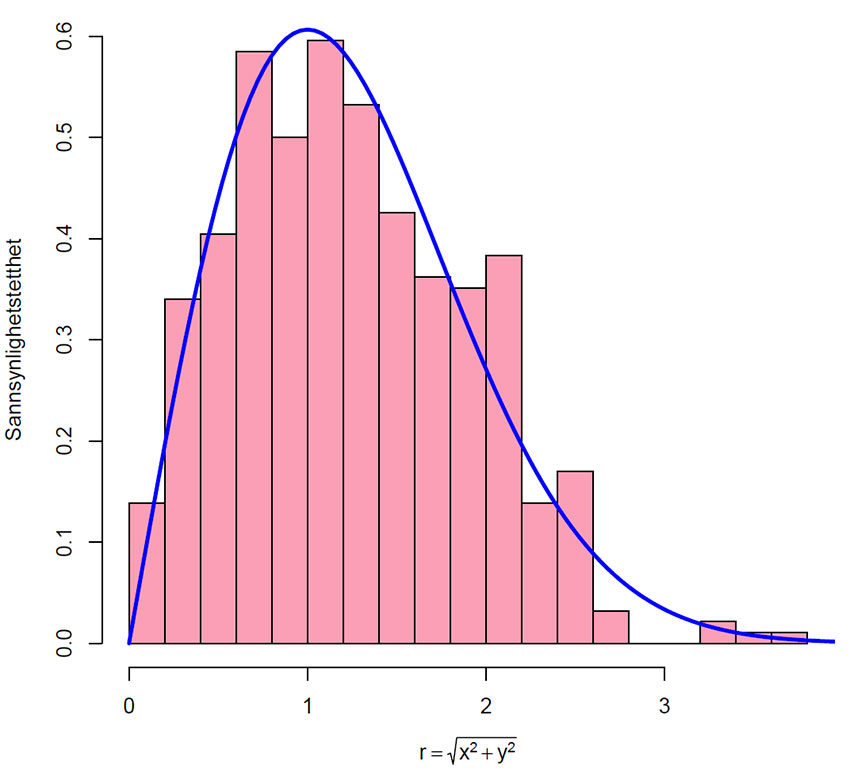
Histogram av radiene fra praktisk eksperiment med pilkast, og heltrukken linje for Rayleighfordelingen. Selv om både x- og y-koordinatene er normalfordelte, blir ikke radiene normalfordelte, og et punktestimat for π=3.12. Hypotesen stemmer godt overens med praksis.
Monte Carlo simulering av π
Monte Carlo simulering er en statistisk simuleringsmetode ved bruk av tilfeldige tall ,videreutviklet av Nicholas Constantin Metropolis (1909-1986) fra ideer til Stanislaw Ulam (1909-1986). Navn etter Monte Carlo, et sentrum for gambling og spill. Metropolis, Enrico Fermi, Ulam var noen av dem som arbeidet under Oppenheimer i Manhattanprosjektet ved Los Alamos. Jfr. Teller-Ulam hydrogenbomben. Metropolis brukte ENIAC, verdens første digitale datamaskin utviklet ved universitetet i Pennsylvania, og i 1952 MANIAC(Mathematical and Numerical Integrator and Computer).
Lager en firkant med sidelengde 2r (r=1) som omgir en innskrevet sirkel med radius r=1. Monte Carlo simulering ved å plukke ut pseudorandome punkter fra en uniform sannsynlighetsfordeling i intervallet [-r, r], og telle opp hvor mange av dem som havner på innsiden av sirkelen. Forholdet mellom punkter som kommer på innsiden av sirkelen og de på utsiden innenfor kvadratet, en geometrisk sannsynlighet, gir et estimat av π.
Arealet av kvadratet (2r)2 /Arealet av sirkel (2π·r2)= π/4. Hvis man lager n tilfeldige punkter innen for kvadratet så vil nπ/4 være på innsiden av sirkelen, det vil si
\(r^2 < x^2 + y^2\)
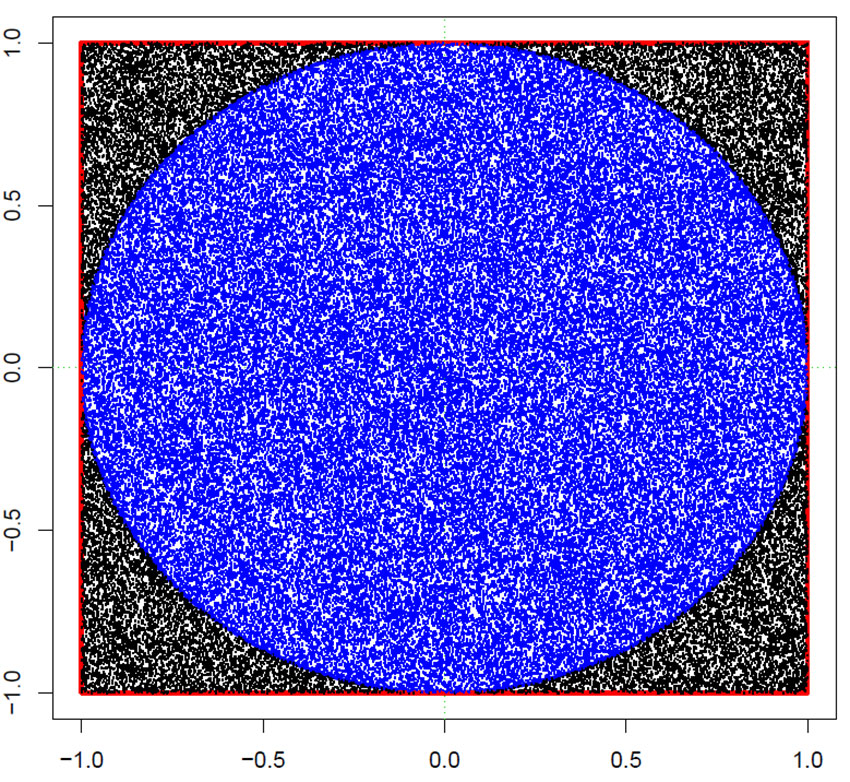
Monte Carlo simulering for et estimat av π hvor 100000 pseudorandome punkter er trukket ut fra en uniform sannsynlighetsfordeling i intervallet [-1, 1]. I denne ene simuleringen vis på figuren ble estimatet for π= 3.14048.
Litteratur
R Core Team (2016). R: A language and environment for statistical
computing. R Foundation for Statistical Computing, Vienna, Austria.
URL https://www.R-project.org/.
Wikipedia