Sannsynlighetstetthetsfunksjonen for standard Cauchyfordeling, f(x, 0,1)::
\(\displaystyle f(x)= \frac {1}{\pi(1+x^2)}\)
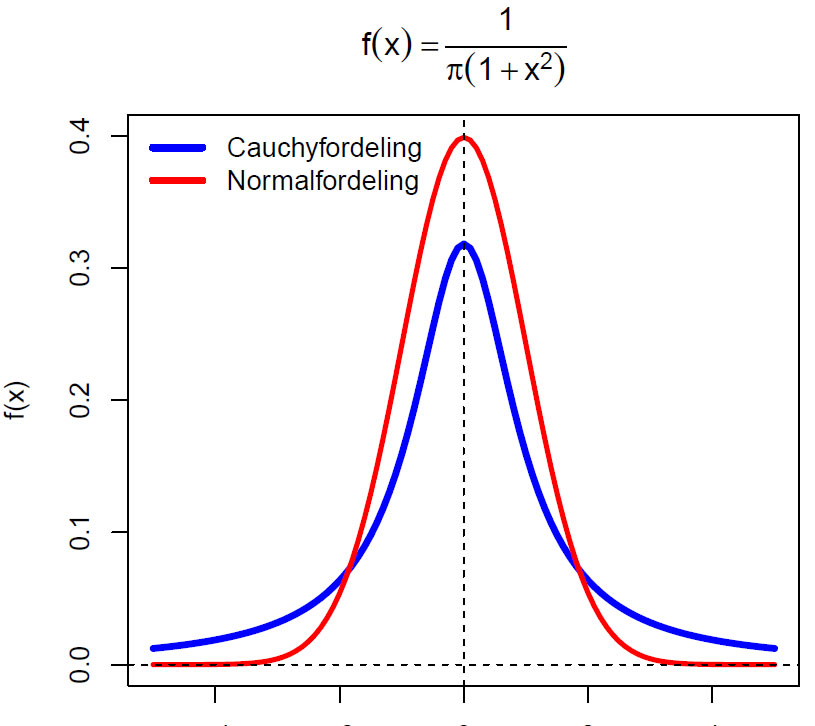
Sannsynlighetstetthetsfordelingen (f(x) for standard Cauchyfordeling, samt standard normalfordeling. (gjennomsnitt=0, og standardavvik=1). Toppen av kurven f(0)=1/π.
Den kumulative sannsynlighetstettheten for standard Cauchyfordeling F(x) er:
\(\displaystyle F(x)= \frac{1}{2}+ \frac{1}{\pi}\arctan (x)\)
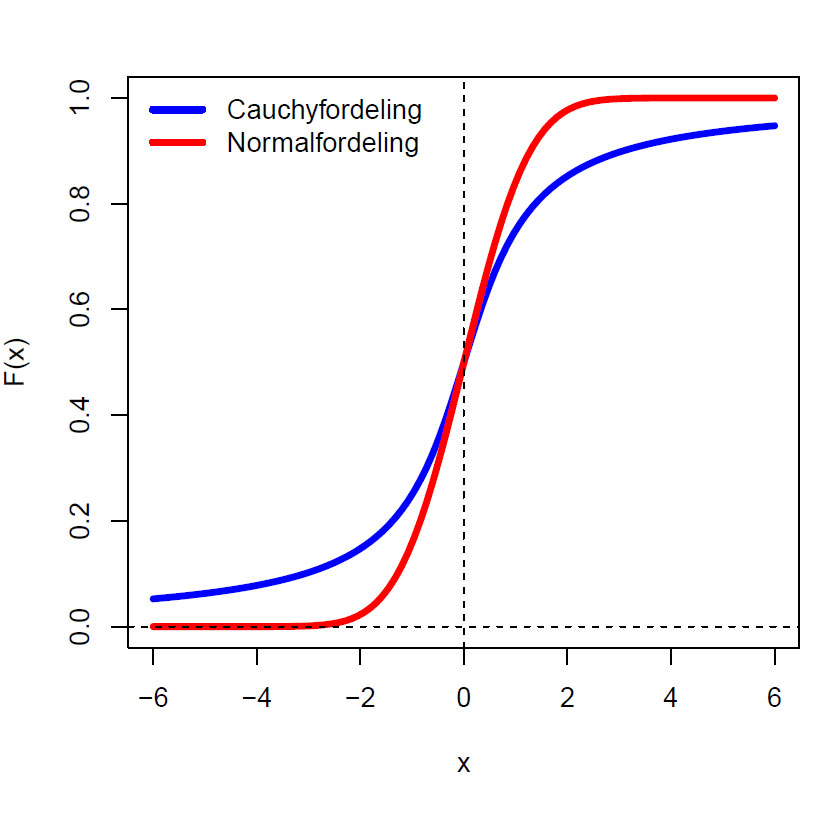
Kumulativ sannsynlighet for standard Cauchyfordeling, samt standard normalfordeling.
Sannsynlighetstetthetsfunksjonen for Cauchyfordleingen:
\(\displaystyle f(x)= \frac{1}{\pi\gamma \left(1+ \left( \frac{x- x_0}{\gamma} \right)^2 \right)}= \frac{1}{\pi\gamma}\left(\frac{\gamma^2}{(x-x_o)^2+ \gamma^2}\right)\)
hvor x0 er en lokaliseringsfaktor som angir hvor man finner topppunktet av fordelingen og gamma (γ) er en skaleringsparameter. som angir halve bredden ved halv maksimum.
Ved standard Cauhcyfordeling vist over er x0=0 og γ= 1
Maksimumsverdien for sannsynlighetstetthetsfunksjonen ved x=x0 er:
\(\displaystyle \frac{1}{\pi\gamma}\)
Den kumulative fordelingsfunksjonen F(X) for Cauchyfordelingen er:
\(\displaystyle F(X)= \frac{1}{\pi} \arctan\left(\frac{x- x_0}{\gamma}\right)+ \frac{1}{2}\)
Cauchyfordelingen har ikke noe gjennomsnitt, og ikke noe varians. Innen fysikk kalles den Lorentzfordelingen.