Vi skal se på differensialligningen:
\(\displaystyle \frac{dx}{dt}= \sin x\)
Den har numerisk løsning;
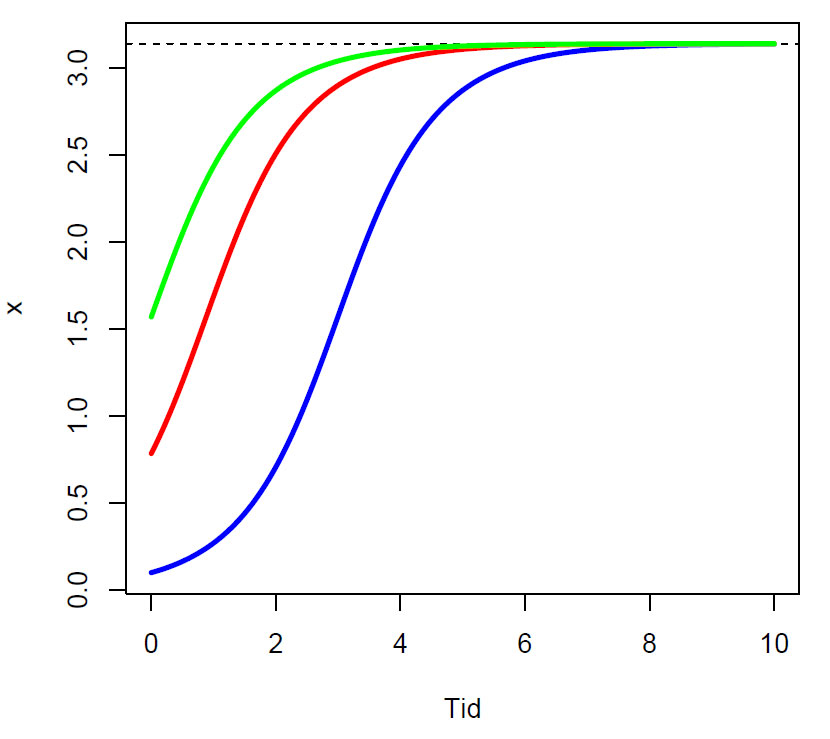
Figur. Løsning av dx/dt=sin x. Initialverdier 0.1 (blå), pi (π)/4 (rød) og pi (π)/2 (grønn). Løsningen nærmer seg pi (π) (stiplet svart linje).
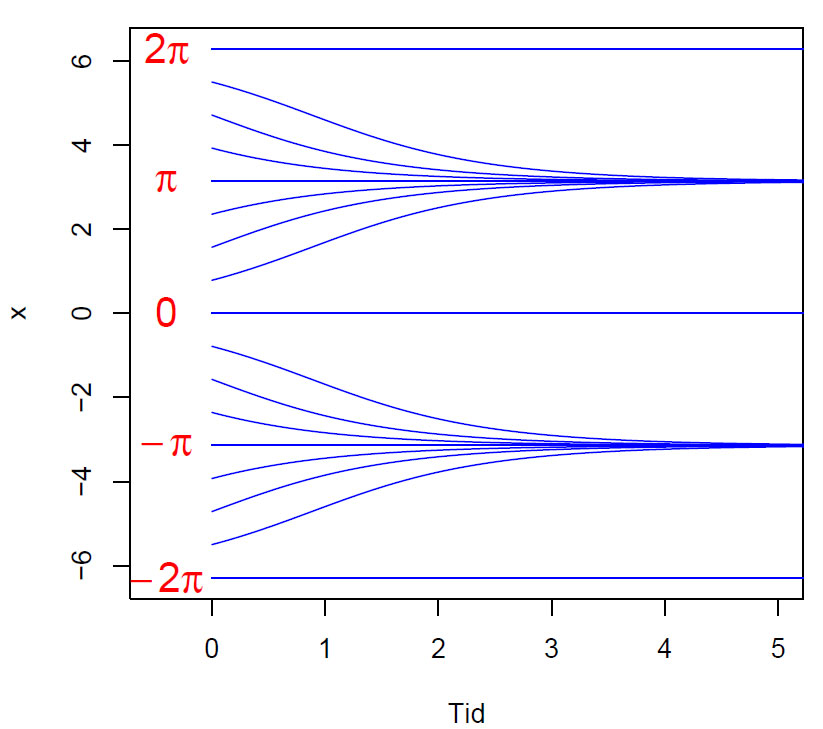
Figur. Numerisk løsning av dx/dt=sin(x) med intialverdier som varierer fra 2π til -2π, hvor π og –π er stabile punkter hvor vektorfeltet nærmer seg, kalt sink eller attraktor, mens 2π, 0 og -2π er ustabile punkter kalt repeller eller kilder.
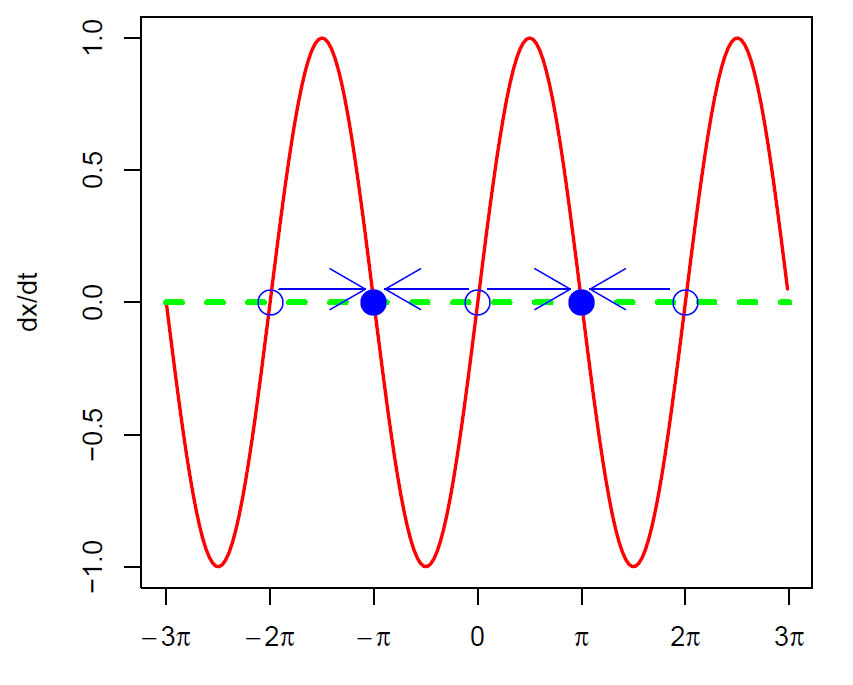
Vektorfeltet framkommer ved at man beveger seg langs x-aksen, men hvor hastigheten endrer seg avhengig av dx/dt=sin(x). Over x-aksen er dx/dt>0 og man beveger seg mot høyre, under x-aksen er dx/dt<0 og man beveger seg mot venstre. Vi ser da samling ved tette blå punkter ved -π til π, og det kan flyte i begge retninger ved de åpne sirkelpunktene -2π, O, 2π. Se pilene.
Analytisk løsning
Den anlytiske løsningen får man ved å atskille variablene:
\(\displaystyle dt= \frac{dx}{\sin x}\)
\(\displaystyle t= \int \csc x dx= -\ln|\csc x + \cot x| + C\)
For de fleste differensialligninger er det umulig å finne den analytiske løsningen.
Litteratur
Regneeksemplet vist over er hentet fra Steven H Strogatz: Nonlinear dynamics and chaos. Perseus Books Publ. 1994, side. 16-18