\(\frac{d^2 y}{dx^2}= xy\)
Dette er en andre ordens differensialligning hvor det er et punkt hvor løsningene skifter fra oscillasjoner til en eksponentialløsning. Den kan omgjøres til to første ordens differensialligninger og løses numerisk.
Airy-funksjonen er lik et integral som konvergerer:
\(Ai(x)=\displaystyle\frac{1}{\pi} \int_o^\infty \cos \left(\frac{t^3}{3}+xt\right)dt\)
Den andre løsningen Bi(x) har lik amplitide og oscillasjon som Ai(x), men er forskjøvet i fase med π/2
\(Bi(x)=\displaystyle\frac{1}{\pi} \int_o^\infty \left[e^{\left(-\frac{t^3}{3}+xt\right)}+\sin \left(\frac{t^3}{3}+xt\right)\right]dt\)
Airy-funksjonen inngår i mikroskopi og astronomi hvor det kommer fram et mønster som skyldes diffraksjon og interferens. Brukt også innen kvantemekanikk hvor en partikkel befinner seg i veldefinert potensialbrønn, en løsning av et spesialtilfelle av Schrödingerligningen. Benytter pakken gsl (GNU Scientific Library) i R som inneholder numeriske rutiner til vitenskapelig bruk.
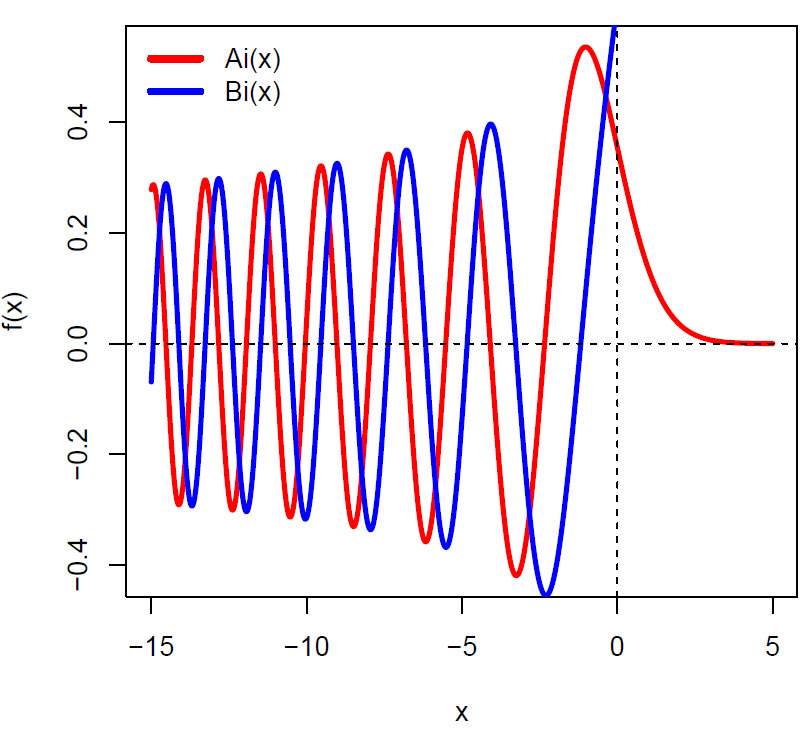
Vi kan også se på Ai(-x):
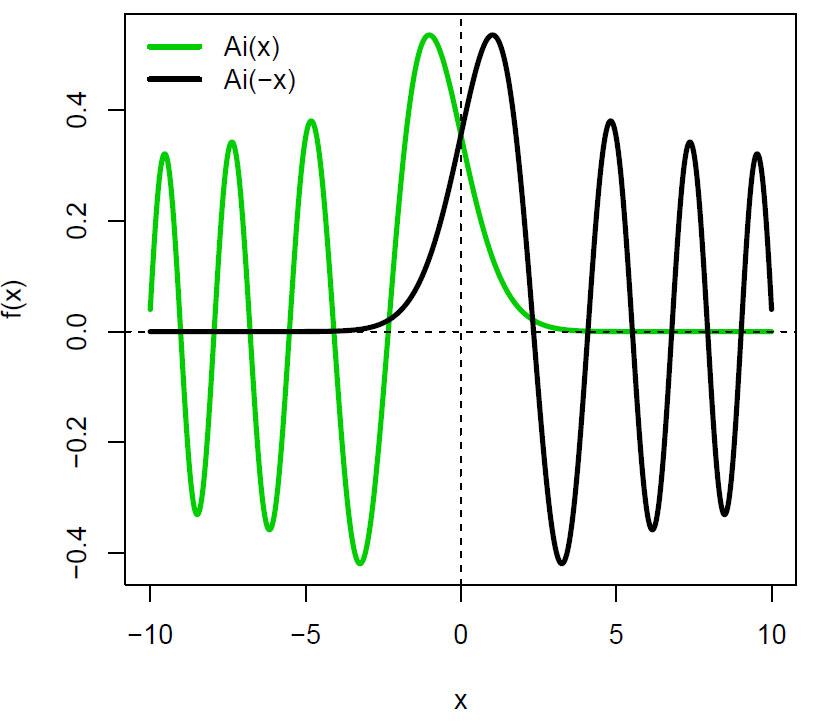
Ved x=0 er Airy-funksjonen:
\(Ai(0)= \frac{1}{3^{\frac{2}{3}}\Gamma \left(\frac{2}{3}\right)}\)
hvor Γ er gammafunksjonen:
Den deriverte av Airyfunksjonen (A’(x)) ved x=0
\(Ai'(0)= \frac{1}{3^{\frac{1}{3}}\Gamma \left(\frac{1}{3}\right)}\)
Verdien for Bairy-funksjonen ved x=0
\(Bi(0)= \frac{1}{3^{\frac{1}{6}}\Gamma \left(\frac{2}{3}\right)}\)
Wronskian for Ai(x) og Bi(x) er lik 1/π.
Den deriverte av Bairy-funksjonen (B’(x)) ved x=0:
\(Bi'(0)= \frac{3^{\frac{1}{6}}}{\Gamma \left(\frac{2}{3}\right)}\)
Vi kan også se på den førstederiverte av Airy-funksjonen (Ai’(x)), som er lik 0 ved maksimums- og minimumspunktene:
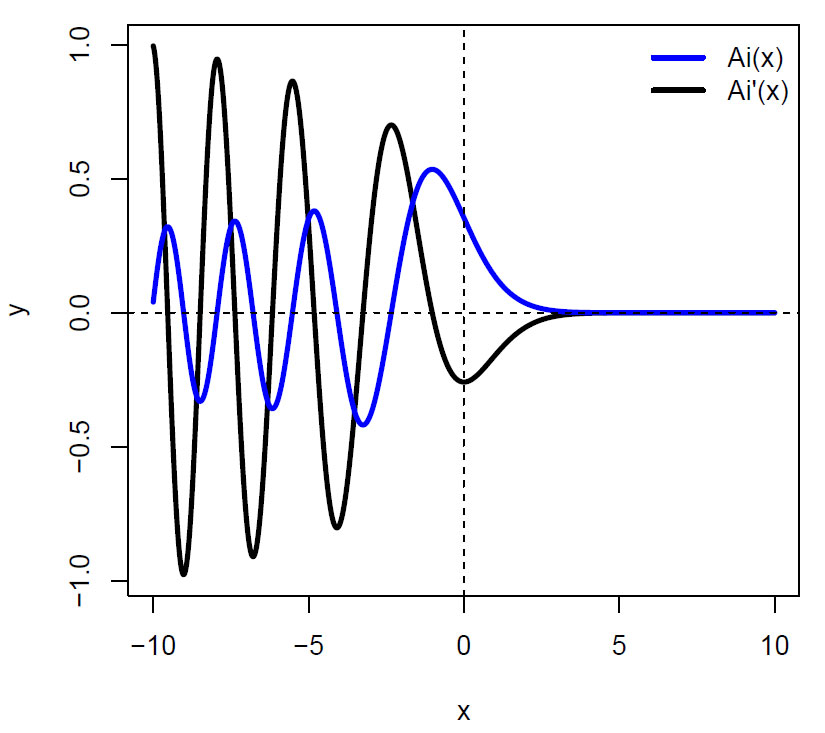
Vi ser på Bairy-funksjon for Bi(x), Bi(-x) og de førstederiverte av disse:
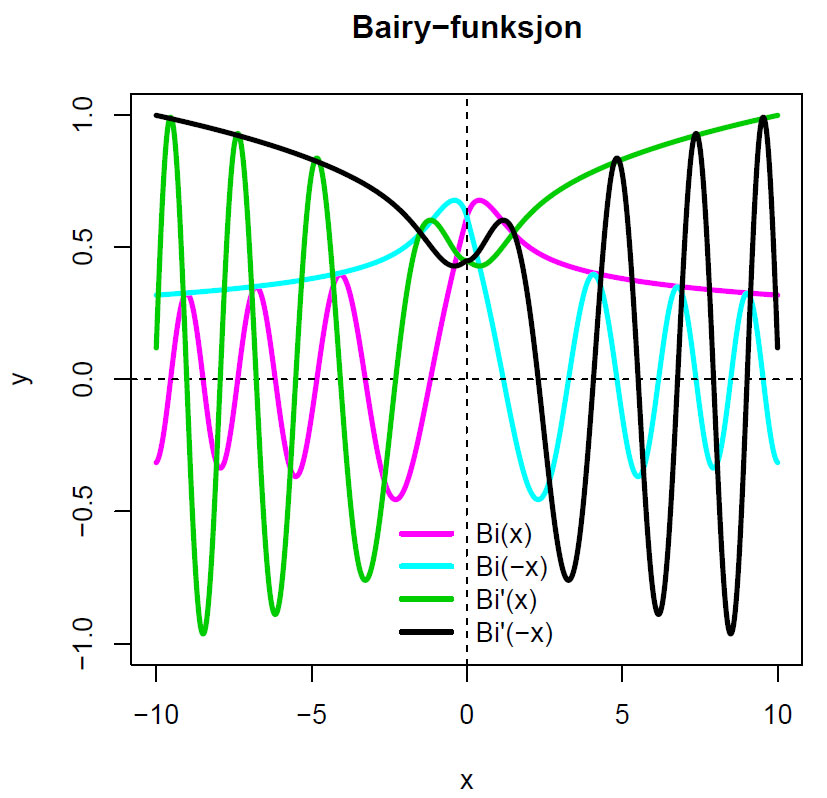
Airy-funksjonen kan utvides til å gjelde kompleksplanet.