Bessels differensialligning:
\(x^2 \frac{d^2 y}{dx^2}+ x\frac{dy}{dx}+ \left(x^2 - \alpha ^2\right)y=0\)
hvor α kan være et komplekst tall, men vanligvis heltall, eller halve heltall, og tallet angir grad eller orden av Bessel-funksjonen. Det er to lineært uavhengige løsninger av differensialligningen. Bessel-funksjoner kalles også sylinderfunksjoner og er løsning av Laplace-ligningen i sylinderkoordinater. Benyttes i utbredelse av lyd, frekvensavhengig friksjon i sirkulære rør, signalprosessering (Besselfilter).
Besselfunksjonen første grad kan uttrykkes som en Taylor-rekke:
\(J_\alpha (x)= \displaystyle\sum_{n=0}^\infty \frac{\left(-n\right)^n}{n!\Gamma\left(n+\alpha+1\right)}\left(\frac{x}{2}\right)^{2n+\alpha}\)
hvor Γ er gammafunksjonen, n! er fakultetsfunksjonen.
Den kan også uttrykkes som et Bessel-integral:
\(J_\alpha (x)= \displaystyle\frac{1}{\pi}\int_0^\pi \cos\left(nt-x\sin(t)\right)dt\)
Besselfunksjonen kan også uttrykkes som en hypergeomtrisk rekke og er tilknyttet Laguerre-polynomer
Besselfunksjonen første grad Jn(x)
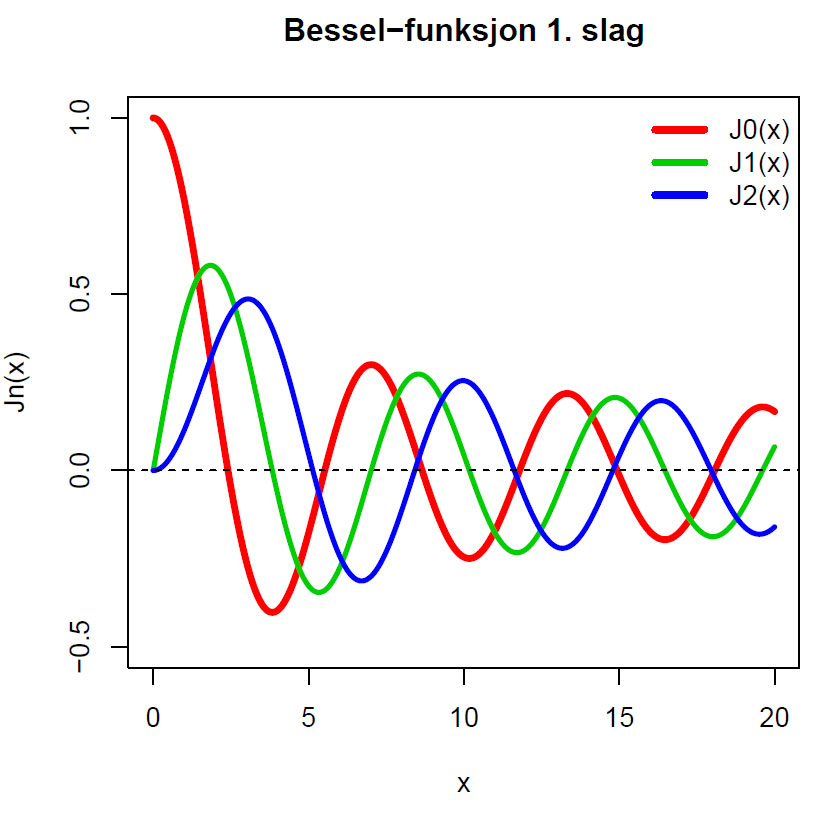
Figuren viser Bessel-funksjonen av første grad Jα(x), hvor α er heltall. Bessel-funksjonen er oscillasjoner som minsker proporsjonalt med 1/kvadratroten(x).

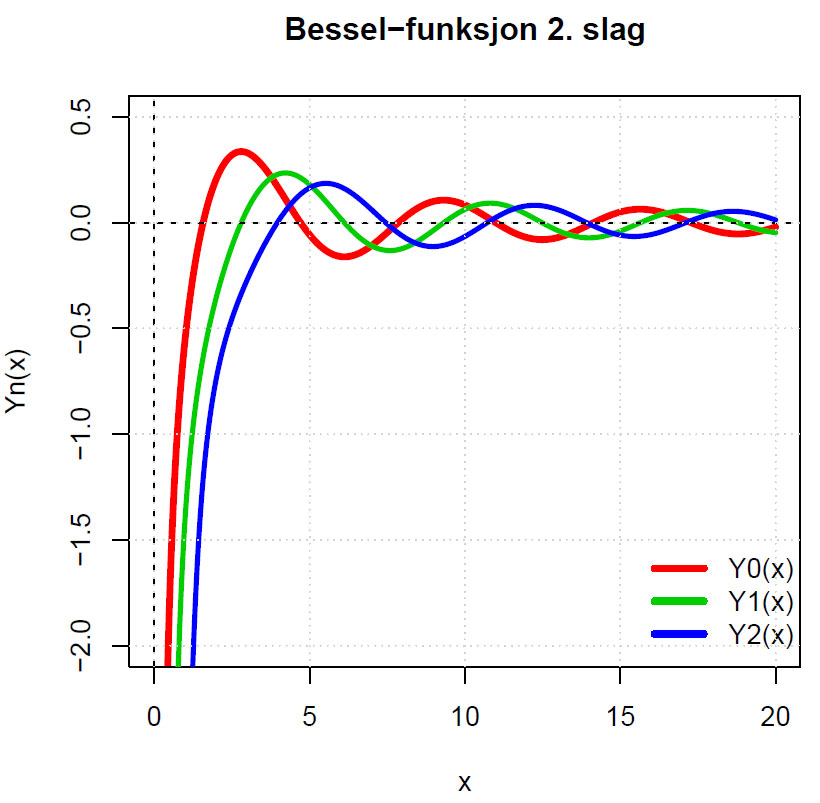
Besselfunksjonen andre slag Yn
Dette er løsninger av Bessel-ligningen som har en singularitet ved x=0. For ikke-heltall har den tilknytning til Jn(x) og kan også uttrykkes som en integralformel. Den kan også benyttes i kompleksplanet, jfr. Hankel-funksjoner.
Modifiserte Besselfunksjoner Iα og Kα
Besselfunksjonen gjelder for komplekse argumenter x, hvor løsningene kalles modifiserte Besselfunksjoner, eller hyperbolske Besselfunksjoner av første og andre slag.
\(I_\alpha (x)=i^{-\alpha} J_\alpha(ix)= \displaystyle\sum_{n=0}^\infty \frac{\left(-n\right)^n}{n!\Gamma\left(n+\alpha+1\right)}\left(\frac{x}{2}\right)^{2n+\alpha}\)
\(K_\alpha(x)= \frac{\pi}{2}\frac{I_{-\alpha}(x)-I_\alpha (x)}{\sin (\alpha \pi)}\)
Besselfunksjoner av første og andre grad kan uttrykkes i form av modifiserte Besselfunksjoner:
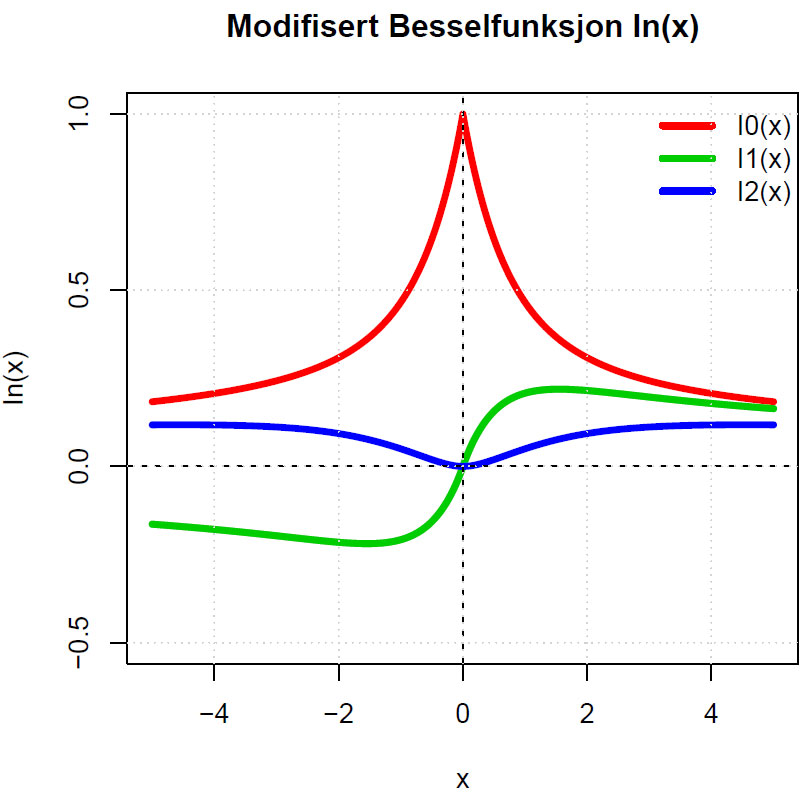
Modifiserte Besselfunksjon In(x):
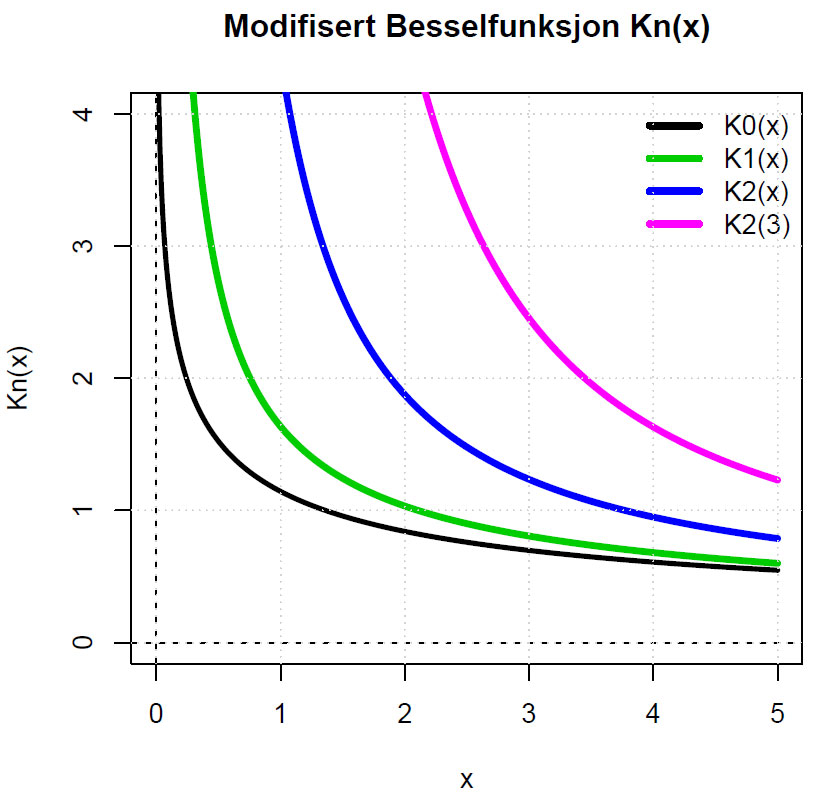
Modifiserte Besselfunksjon Kn(x) :
Det finnes også sfæriske Besselfunksjoner jn og yn.