Thales fra Milet brukte geometri for å beregne høyden av pyramidene, og hvor langt et skip befant seg fra kysten. Pytagorerene fant bevis for det pyragoreiske teorm.

Koordinatsystem
Alle punkter i planet P=(a,b) bestemmes i forhold til to cartesiske koordinatakser (oppkalt etter Descartes) som står normalt på hverandre, hvor a tilsvarer x-koordinaten og b er y-koordinaten. De to koordinataksene deler det todimensjonale planet inn i fire kvadranter I-IV hvor første kvadrant (I) er øverst til høyre og deretter nummerert mot klokken.

Punktene P(1,2) og Q(3,3) i planet.
Vi kan finne avstanden (d) mellom to punkter P=(x1,y1) og Q=(x2,y2) i planet ved å bruke Pythagoras:
\(d=\sqrt{(x_2-x_1)^2+ (y_2-y_1) ^2}\)
For å kunne trekke en linje er det nok å kjenne stigningskoeffisienten (”slope”) β1 og punktet P=(x1,y1) som linjen går igjennom:
\(y= \beta_ 1(x-x_1)+ y_1\)
En linje kan også uttrykkes i form av stigningstall β1 og skjæringspunkt β0 med y-aksen (”intercept”).
\(\beta_1=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}\)
\(y=\beta_0 + \beta_1 x\)
eller hvis du foretrekker det må du gjerne kalle den rette linjen:
\(y= a + bx\)
hvor a er skjæringspunktet med y-kasen og b er stigningstallet eller stigningskoeffisienten for linjen.
Euklids aksiomer
Euklid startet på 300-tallet f.kr. å lage et sett med aksiomer og postulater om punkter (uten utstrekning), linjer og sirkler. Det tredimensjonale rom kalles det Euklidske rom.
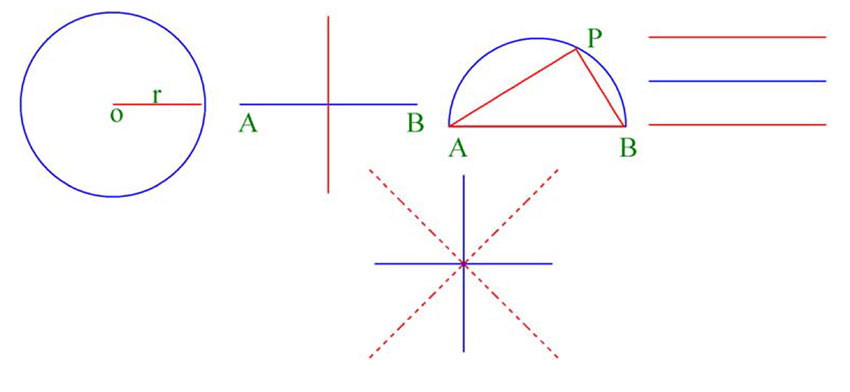
Punkter med avstand r fra et punkt o (origo) ligger på en sirkel med sentrum i o og radius r.
Alle punkter som ligger like langt fra A og B ligger på en linje på midtnormalen.
Punkter P som danner en rettvinklet trekant blir liggende på en sirkel.
Det som ligger like langt fra en rett linje ligger på linjer som er parallelle med den gitt linjen.
Halveringslinjene til to gitt linjer inneholder punktene som er like langt fra hver av linjene.
Paralellaksiomet gjelder ikke i hyperbolsk geometri.
De klassiske problemstillingene i geometri har vært sirkelens kvadratur, kubens fordobling og vinkelens tredeling.
Sirkelens kvadratur er problemstillingen å konstruere et kvadrat med samme areal som en sirkel. Hvis vi lar radius=1 og x er sidelengden i kvadratet må følgende ligning være oppfylt, og man skjønner vanskeligheten med å konstruere π:
\(x^2=\pi r^2 \;\;\; \implies \;\;\; x^2 = \pi \;\;\; \implies \;\;\;\; x=\sqrt{\pi}\)
Opprinnelig hadde geometrien praktisk funksjon i landmåling og arkitektur. Det er noe konkret å konstruere geometriske figurer med passer, blyant og linjal, men geometrien er også abstrakt.
Gresk matematikk var i mange sammenhenger synonymt med geometri og navn som Euklid, Arkimedes (287-212 f.kr., Arkimedes skrue, legemer og oppdrift i vann, vektstangprinsipp, Heureka), Heron fra Alexandria(ca. 250 f.kr.), Eratosthenes (275-194 f.kr., E.´s sil/sold for å finne primtall, gradmåling mellom Alexandria, hvor han var bibliotekar, og Syene, Jordens omkrets) og Apollonios fra Perga (ca. 230 f.kr., kjeglesnitt). Seinere kom det viktige bidrag fra Euler, Gauss og Nikolay Ivanovitsj Lobasjevskij (1792-1856),sistnevnte bl.a. med hyperbolsk geometri (ikke-Euklidsk geometri) hvor parallellaksiomet ikke gjelder.
Innen klassisk Euklidsk geometri er det spesielle punkter knyttet til en trekant ABC med sidene a,b,c og vinklene α, β og γ.

Ortosenter (Arkimedes punkt) O er snittet av de tre høydene som står normalt på hver sidekant.
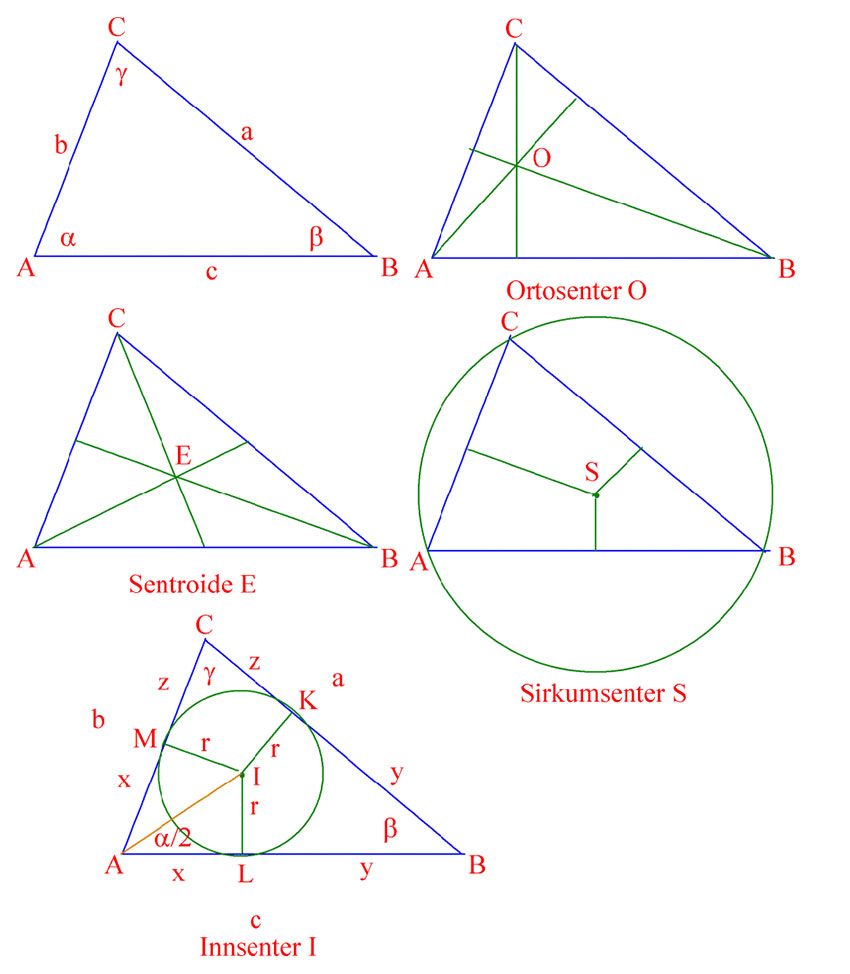
Hvis vi lar linjer gå fra hvert hjørne som deler motstående side på midten så vil disse skjære hverandre i et punkt E kalt sentroide, og som også deler linjene i 2/3 og 1/3, og tilsvarer trekantens tyngdepunkt. Hvis vi omskriver en trekant (triangel) med en sirkel så vil origo i sirkelen være i punktet sirkumsenter (S). Linjer som står normalt på sidekantene vil skjære hverandre i sirkumsenter. Linjene AS=BS=CS=radius i sirkelen. Vi kan la en sirkel være innskrevet i trekanten. Senteret i denne sirkelen kalles for innsenter. Innsenter er også skjæringspunktet mellom de tre linjene AI, BI og CI som halverer henholdsvis vinklene α,β og γ, og disse tre linjene deler den opprinnelige trekanten i tre undertrekanter AIB, BIC, og CIA.
Arealet av den store trekanten ABC blir lik summen av de tre undertrekantene:
\(\text{Areal}\;\;\Delta ABC=\frac{1}{2}cr + \frac{1}{2}ar + \frac{1}{2}br =\left(\frac{a+b+c}{2}\right)r=rs\)
Lengden a+b+c er perimeter og halvparten av denne (a+b+c)/2 kalles semiperimeter og arealet av trekant ABC blir lik radius av innsirkel ganger semiperimeter. Linjer fra innsenter som står normalt på hver sidekant (IK, IL og IM) deler linjene a, b og c i dellinjene x, y og z.
Herons formel sier at arealet av en trekant ABC med lengde av sidekantene a, b og c, og semiperimeter s blir:
\(\text{Areal}\; \Delta ABC=\sqrt{s(s-a)(s-b)(s-c)}\)
Heron har sitt navn knyttet til springvannet Herons brønn og Herons kule, og skrev verker som Metrica, Geometria, Stereometrica, Definitiones, Dioptra (landmåling) og Catoptrica (refleksjon).

Sirkel
En sirkel med sentrum i origo og radius r, og 0≤θ≤2π kan beskrives som polarkoordinater:
\(x=r\cos \theta\;\;\;\; y=r \sin \theta \;\;\;\; x^2 + y^2= r^2 \)
Hvis sentrum i sirkelen ligger i (x0,y0) så har vi:
\(x=x_0 +r\cos \theta\;\;\;\; y=y_0 + r \sin \theta \;\;\;\; (x-x_0)^2 + (y-y_0)^2= r^2 \)
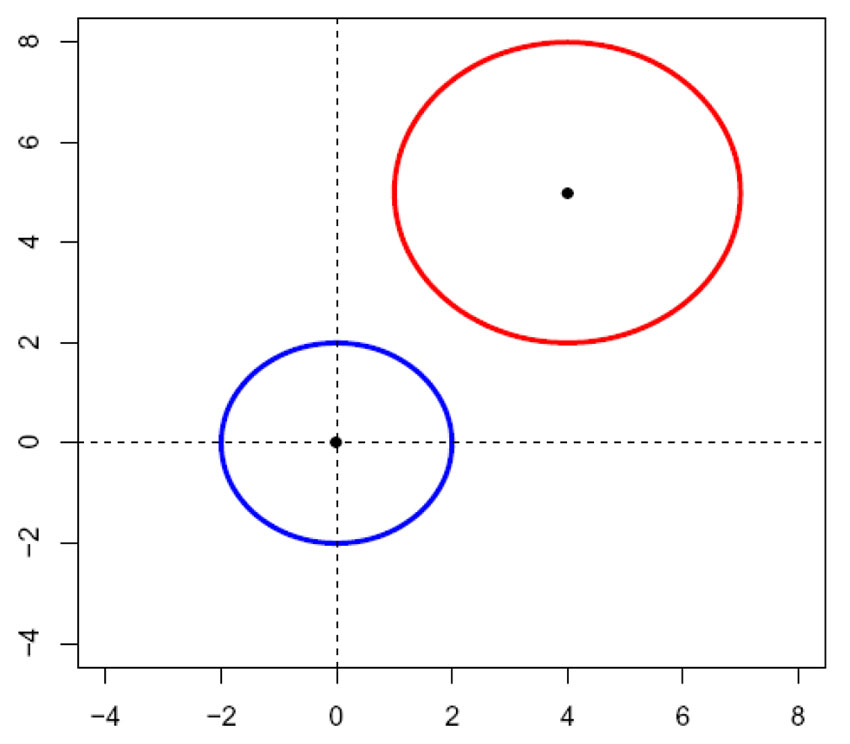
Sirkel med sentrum i origo (0,0) og radius=2, og sirkel med sentrum i (4,5) og radius = 3.
Vi kan generelt finne avstanden d mellom to punkter A=(x1,y1) og B (x2,y2) i planet:
\(d=\sqrt{(x_2-x_1)^2+ (y_2-y_1)^2}\)
For eksempel avstanden mellom A(-1,2) og B(-1,-1): 3
Areal
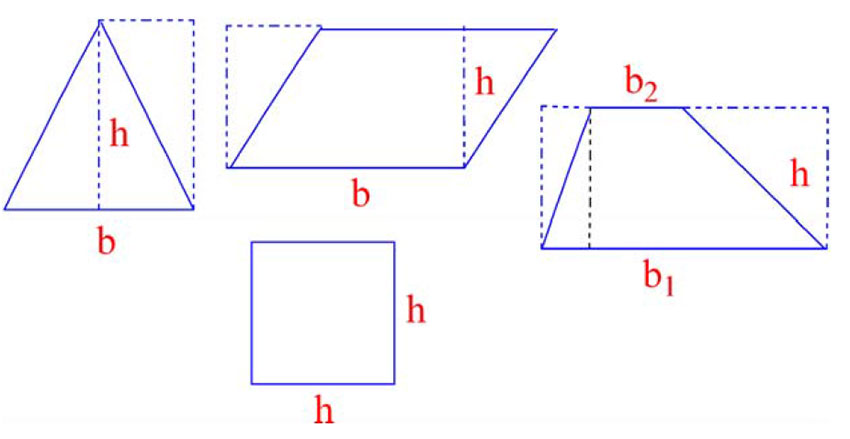
Areal (A) av et kvadrat med like sider h:
\(A=h^2\)
Arealet av trekant med bredde b og høyde h:
\(A=\frac{1}{2}bh\)
Areal av parallelogram:
\(A=bh\)
Areal av trapes:
\(A=\frac{1}{2}(b_1+b_2)h\)
Pythagoras setning: I en rettvinklet trekant hvor a og b er hosliggende sider og c er motstående side (hypotenusen) så er:
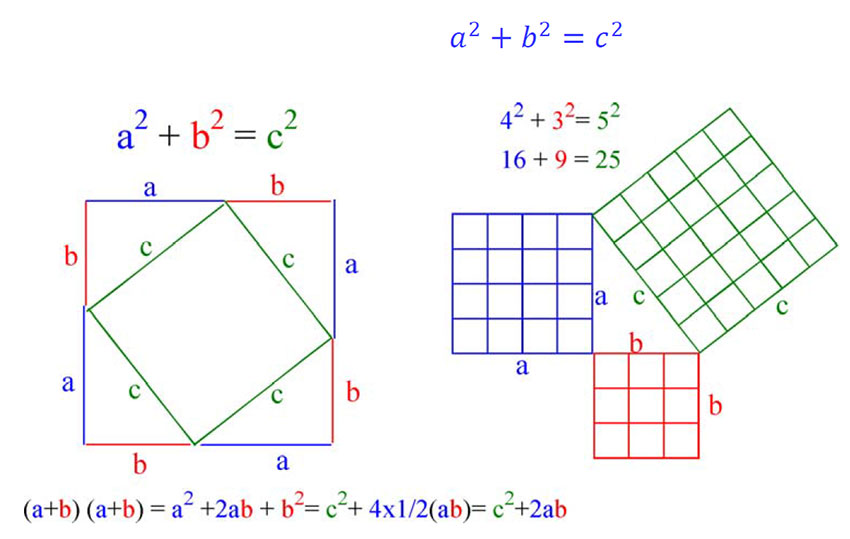

For en vilkårlig trekant med hypotenus c og vinkel θ motstående til hypotenusen gjelder:
\(c^2=a^2 +b^2 - 2ab\cos \theta\)
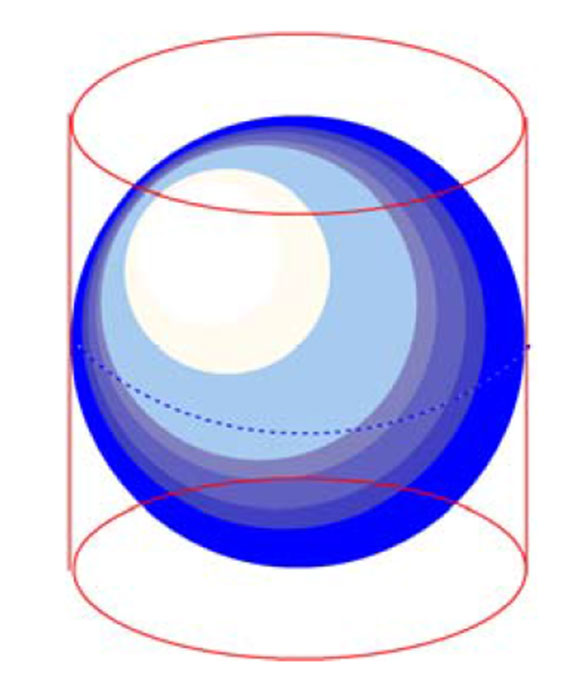
Overflate og volum av en kule med radius r er henholdsvis:
\(\text{Overflate kule}= 4 \pi r^2\)
\(\text{Volum kule}= \frac{4}{3} \pi r^3\)
En sylinder med lengde l og radius r har overflate (inkludert begge ender) og volum henholdsvis:
\(\text{Overflate sylinder}= 2 \pi r^2\;+\; 2\pi rl\)
\(\text{Volum sylinder}= \pi r^2 l\)
Arkimedes fant at hvis man hadde en kule omskrevet av en sylinder, i dette tilfelle er l=2r,
så er overflatearealet av kula 2/3 av overflaten av sylinderen (inkludert begge ender 1.5 ganger større enn overflaten av kula, dessuten volumet av sylinderen er lik 1.5 ganger volum av kula.
Det vil si at forholdet mellom overflatearealene har samme forhold som mellom volumene. Arkimedes fikk ifølge Cicero symbolet med kule og sylinder (inerat sphaerae figura et cylindri) innhugget i sin gravmonument.
Innen gresk matematikk var Euklid, Arkimedes og Apollonius dominerende. Appolonius fra Perga f. 230 f.kr. utviklet teorien om kjeglesnitt, plane snitt gjennom en kjegle som gir elipse, parabel eller hyperbel. Matematisk astronomi med bruk av trigonometri ble ivaretatt av Eudoxus fra Knidos (409-356 f.kr.), Hipparkhos (190-125.f.kr.) og Ptolemeios.
Da det Vestromerske rike kollapset i 476 holdt den greske matematikk seg levende i det Byzantinske eller Østromerske rike med senter i Konstantinopel. I det Vestromerske rike ble det stopp i den vitenskapelige framgangen. Justitian stengte Platons akademi i Aten i 529, som ble betraktet som hedensk. Grekerne ville ha presise begreper, noe som gjorde det vanskelig å arbeide med begrepet uendelig og irrasjonale tall. Uendelighet og uendelige rekker ble et tema for middelalderens matematikere og filosofer. Betegnelsen var kronglete og verbalt beskrevet S quadratus og S cubus ble mye enklere skrevet som S2 og S3, og det var den franske matematikeren François Viète (1540-1603) som innførte det matematiske symbolspråket, og skrev bl.a. Opera mathematica (1646). Det tok ennå noe tid før symbolet = for likhetstegnet (aequalis) ble tatt i bruk.
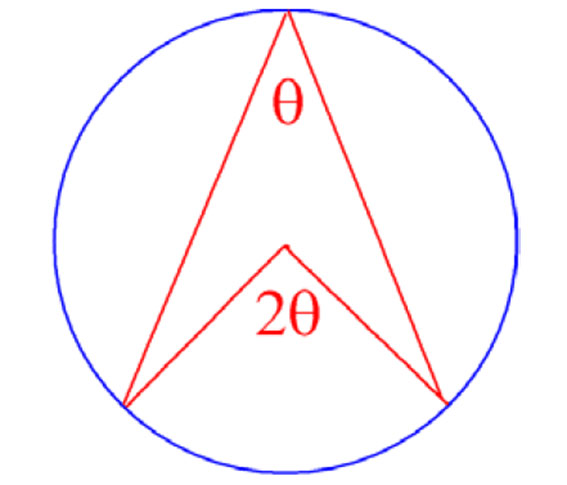
Hvis vi har et punkt på sirkelen med to lange vinkelbein som danner en periferivinkel theta (θ) med hverandre, så vil vinkelen fra radius være 2θ.