Kardinalsinusfunksjonen sinc (sinus cardinalis) er definert som unormalisert sincfunksjon:
\(sinc\; x= \frac{\sin x}{x}\;\;\;\;\; x\neq 0\)
I digital signalbehandlingen defineres den som normalisert sincfunksjon:
\(sinc\; x= \frac{\sin \pi x}{\pi x}\)
Den normaliserte sinc-funksjonen er lik 0 ved heltallsverdier:
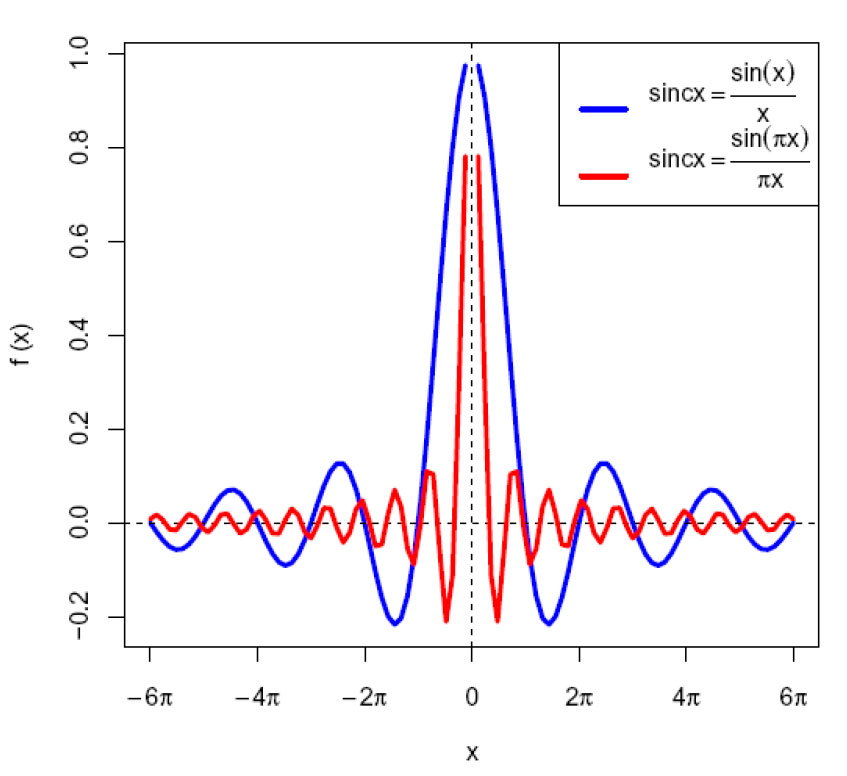
sinc-funksjonen
Den unormaliserte sinc(x) har skjæring med x-aksen der hvor cosinusfunksjonen har sine maksimums- og minimumsverdier.
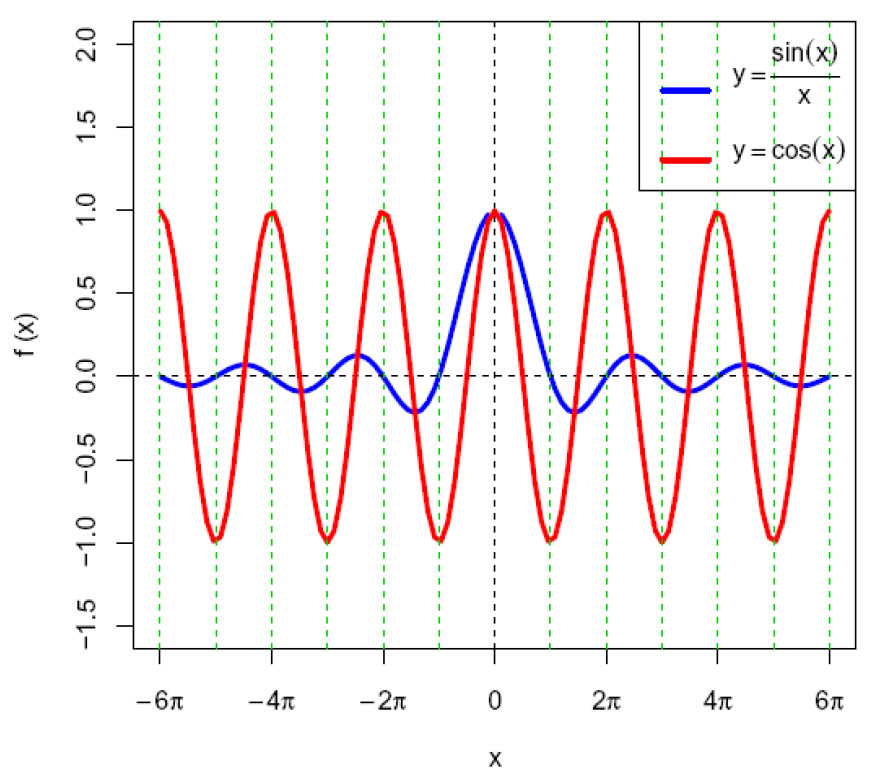
Sinc- og cosinus-funksjon.
Euler oppdaget følgende produktsammenheng mellom den unormaliserte sinc-funksjonen og et uendelig produkt av cosinus:
\(\frac{\sin x}{x}=\displaystyle\prod_{n= 1}^\infty \cos \left(\frac{x}{2^n}\right)\)
Det er også et sammenheng mellom den normalisert sinc-funksjonen og et uendelig produkt:
\(\frac{\sin \pi x}{\pi x}=\displaystyle\prod_{n= 1}^\infty \left(1-\frac{x}{n^2}\right)\)
Den normalisert sinc-funksjonen er også relatert til gammefunksjonen (Γ):
\(\frac{\sin \pi x}{\pi x}= \frac{1}{\Gamma(1+x)\Gamma(1-x)}\)
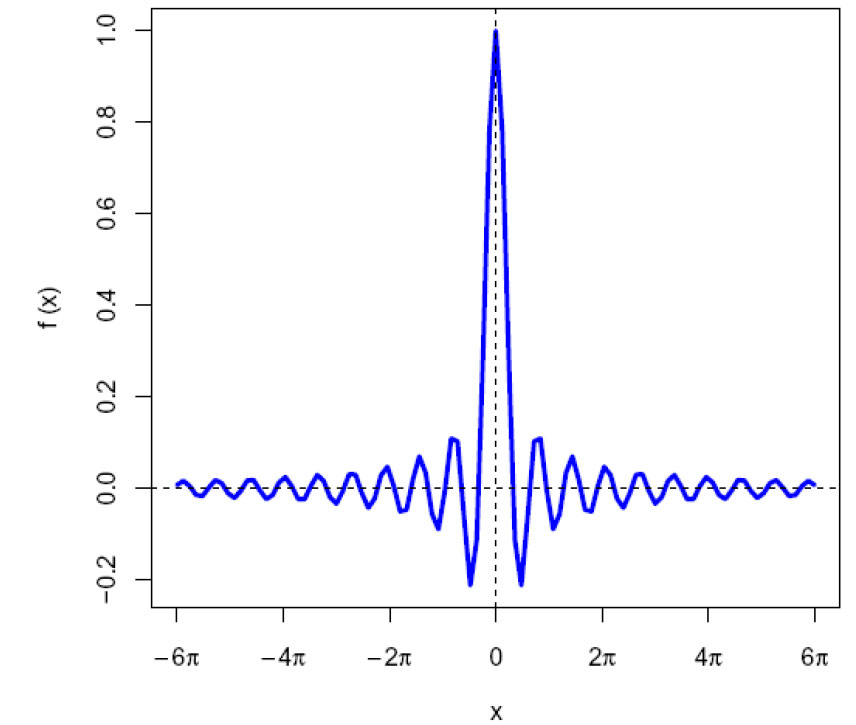
Normalisert sincx uttrykt som gammafunksjon.
Rektangelfunksjonen
Det er en sammenheng mellom Fourier-transformasjon av rektangelfunksjonen og sinc(x)-funksjonen.
\(\\rect(x) = \begin{cases} 0 & \quad \text{hvis} \; |x| >\frac{1}{2}\\ \frac{1}{2} & \quad \text{hvis}\; |x|=\frac{1}{2}\\ 1 &\quad\text{hvis}\; |x|<\frac{1}{2} \end{cases} \)