En torus er en smultringformet struktur:
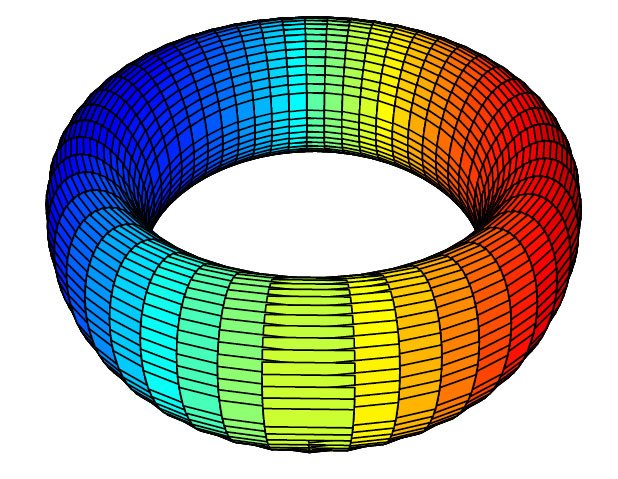
En torus med koordinatene:
\(\displaystyle x= (c+a \cdot \cos \phi)\cdot \cos \theta\;\;\;\;\; y= (c+a \cdot \cos \phi)\cdot \sin \theta\;\;\;\; z= a\cdot \sin \phi\)
og vinklene phi (φ) og theta (θ) i 2π radianer. Når konstantene c og a er like får torusen en kuleform, men det er fremdeles hull i den.
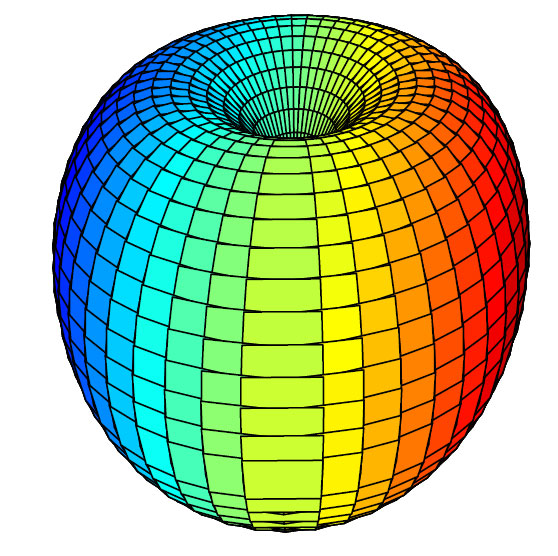
Torus hvor konstantene c=a, får form som en kule med hull i midten, og er en homomorf med smultringen.

En kopp med hank er homomorft med en smultring (torus). Tallerken danner en ring uten hull og er en annen hovedtype topologisk objekt. En sirkel og et kvadrat er topologisk like.
Topologiske kart
T-banesystemet i Oslo er eksempel på et system hvor mønster og knutepunkter blir riktig, men avstander og geografi blir feil. Dette er et viktig prinsipp i studiet av topologi.
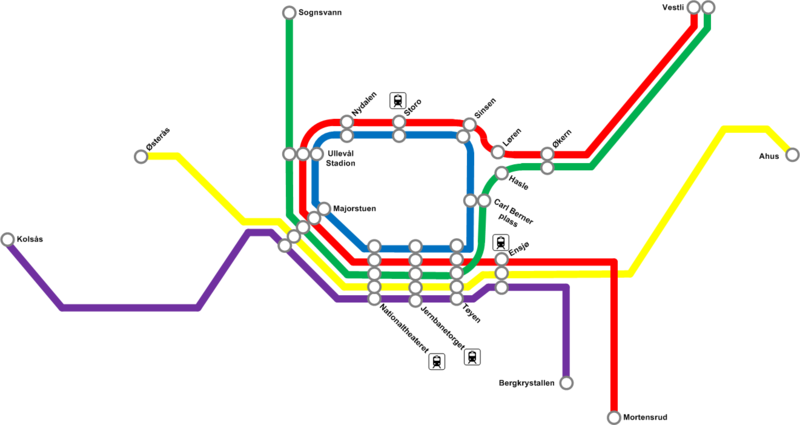
Topologisk kart over T-banen i Oslo. Angir ikke riktige avstander og størrelser, men bare den todimensjonale presentasjonen av holdeplasser (noder) og linjer.
Topologi anvendt innen beskrivelse av nett og nettverk av veier, turveier og gater, Topologisk nettverkoffentlig kommunikasjon (Linjer og stasjoner for tog, busser, trikker og T-baner. Topologi innen strømnett med sjøkabler, høyspentledninger og lavspentnett med tofase eller trefase fram til boliger og industri. Datakabler med fibernett og knutepunkter for rutere og datasvitsjer.
Topologi i DNA, RNa og protein
DNA, RNA og proteiner danner tredimensjonale topologiske strukturer. Superkveilet DNA og pakket kan beskrives som topologisk struktur i form av lenketall.
Polygoner, polyedre og Euler-karakteristikk
Hvis vi tegner et nettverk av punkter (P)(eller hjørner H) og linjer (L) som danner flater (F) med trekanter så viste Euler at det var følgende sammenheng mellom antallet linjer punkter og flater(Eulerkarakteristikk), K er antall kanter:
\(H-K+F=2\)

I regulære polygoner (regulære mangekanter) har alle sidene lik lengde og alle vinklene er like. I Euklids Elementer omtales punkter (uten utstrekning), linjer, flater og fastelegemer. En rekke punkter danner en linje.
Euklids Elementer (Stoikheia) i matematikk (geometri, tallteori) er bygget opp av definisjoner og aksiomer (postulater), matemtiske setninger og bevis. Euklid levde ca. 300 år fvt. i Alexandria Stoikheia ble oversatt til arabisk og seinere latin og danner også basis for logikk og filosofi. Euklids postulater danner basis for Euklidsk geometri med punkter, linjer og sirkler. Geometriske konstruksjoner med passer og lineal, samt de mer avanserte kjeglesnitt. Mellom to punkter kan det bare trekkes en rett linje. En Linje kan forlenges i begge retninger. Omkring ethvert punkt kan det trekkes en sirkel med en radius. Alle rette vinkler er like. Det femte postulat er parallelpostulatet om at to parallelle linjer aldri vil skjære hverandre hvis de forlenges. Euklids bevis for den pytagoreiske læresetningen.
Uansett hvordan man tegner streker som krysser hverandre kommer man alltid opp til å ende opp med at H-K+F=2. Når det gjelder den lukkete trekanten har den 2 flater eller regioner, en på innsiden og en på utsiden.
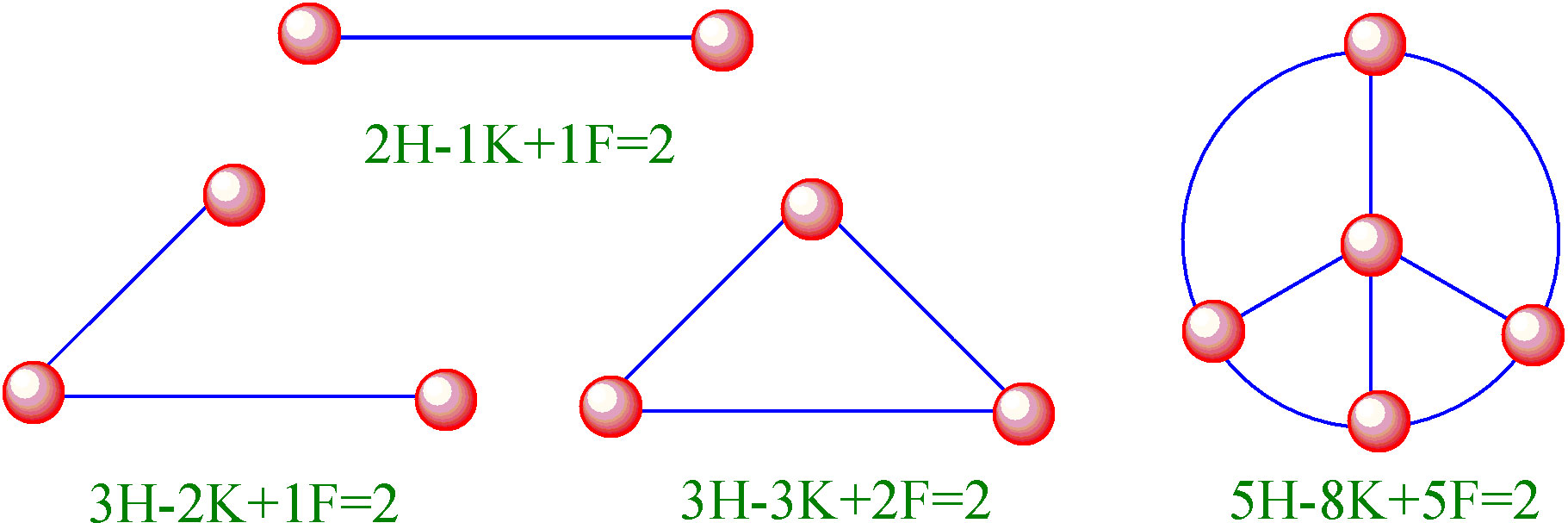
Eulers polyederformel viser sammenhengen mellom antall hjørner, kanter og flater på faste legemer, noe man kan finne igjen i pyramider, prismer og krystaller.
En kube har 6 flater, 12 kanter og 8 hjørner.
Polygoner kan klassifiseres etter hvor mange kanter og flater, lengden av kanter og vinkelen mellom dem. En fotball består av 12 femkanter og 20 sekskanter.

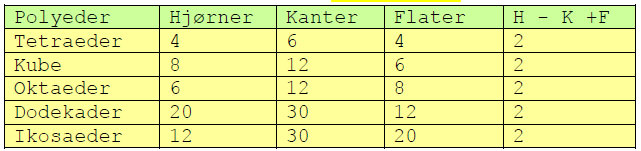
Regulære polygoner, alle med Eulerkarakteristikk=2

Simon-Antoine-Jean Lhuilier (1750-1840) fant i 1913 unntak fra Eulers polyederformel hvis det var et hull i et objekt.
En kule er den enkleste formen i et tredimensjonalt rom. En kule og en torus er hule overflater. Hullet i en torus (smultring) er ikke på overflaten, men i det omliggende rom. Verken kule eller torus har noen kanter, og begge har en lukket overflate.
I et tredimensjonalt nettverk kan nettverkstrådene gå over eller under hverandre, men det er ikke mulig i et todimensjonalt hvor de må krysse hverandre.
Hvis vi lager nettverket på en kule, for eksempel på en appelsin blir sammenhengen den samme:
\(H-K+F=2\)
En sirkel kan betraktes som et uendelig mangesidet polygon. Tredimensjonalt blir sirkelen en symmetrisk kule. Den korteste vei mellom to punkter på en kule er storsirkelen, en sirkel med sentrum i kloden og omkrets like lang som ekvator. Korteste vei mellom to punkter på en fly- eller båttur er å følge en storsirkel. Tegner man en trekant i et plan er summen av vinklene =180o. Tegner man en trekant på en kule, for eksempel på skallet på en appelsin er summen av vinklene = 270o. Tegner man en trekant på en sadel er summen av vinklene <180o.
Det er 5 regulære polyedere, også kalt Platonske kosmiske legemer. Disse ble tidligere tillagt mytisk kraft og finnes bl.a. igjen i Keplers Mysterium cosmographicum.
Tetraeder (4 identiske trekanter)
Kube (6 identiske firkanter)
Oktaeder (8 like trekanter)
Dodekader (12 pentagoner)
Ikosaeder (20 like trekanter)
Den ytre pakkingen av proteiner i kapsidet hos virus er ofte formet som et ikosaeder.
Ifølge Platons Timaios tilsvarte tetraeder-ild,kube-jord, oktaeder-luft, dodekader-universet, og ikosader-vann
Det er en sammenheng mellom antall hjørner (H), kanter (K) og flater (F) beskrevet, hvor alle har Eulerkarakteristikk lik 2.
De regulære polyedere er kompakte legemer. En torus er en smultringformet yttergrense med ett hull. En torus har en annen Eulerkarakteristikk enn de regulære polyedere. Topologisk sett er det meget stor forskjell på yttergrensene på en hul kule sammenlignet med yttergrensene på en torus.
De regulære polyedere er kompakte legemer. En torus er en smultringformet yttergrense med ett hull. En torus har en annen Eulerkarakteristikk enn de regulære polyedere. Topologisk sett er det meget stor forskjell på yttergrensene på en hul kule sammenlignet med yttergrensene på en torus.
For en torus er Eulerkarakteristikken:
\(H-K+F=0\)
En dobbeltorus har Eulerkarakteristikk -2.
En Klein-flaske har Eulerkarakteristikk lik null (0). Navn etter den tyske matematikeren Christian Felix Klein (1849-1925) som bl.a. ga viktige bidrag til geometri med sitt Erlangen Program som kombinerer Lie-grupper (Sophus Lie) og ikke-euklidsk geometri.
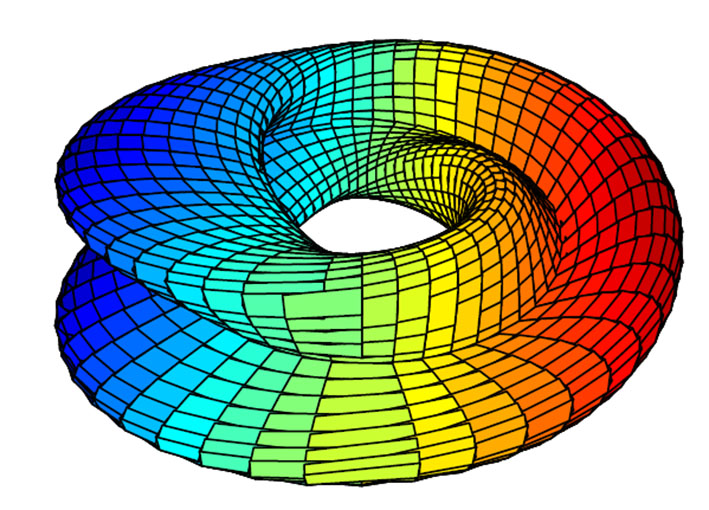
Figur8-torus av en immersjon av en Klein-flaske med utgangspunkt et Möbius-bånd. En Klein-flaske representerer et tredimensjonalt Möbius-bånd. r= 2
\(\displaystyle x= \left(r+ \cos\frac{\theta}{2} \sin \phi-\sin \frac{\theta}{2}\sin2\phi \right) \cos \theta\)
\(\displaystyle y= \left(r+ \cos\frac{\theta}{2} \sin \phi-\sin \frac{\theta}{2}\sin2\phi \right) \sin \theta\)
\(\displaystyle z= \sin \frac{\theta}{2}\sin \phi + \cos \frac{\theta}{2}\sin2\phi\)
\(\displaystyle 0 \leq \theta \lt \pi \;\;\; \;\;0 \leq \phi \lt \pi \;\;\;\;\; r \geq2\)
En kule og en torus har ingen kanter og er en lukket overflate. Objekter kan bli transformert ved bøyning, vridning, strekning og sammenpressing. Hvis vi ikke visste bedre er det umulig å si om vi lever på en torus eller en klode. På begge ville området vi befinner oss på være relativt flatt, og går vi rundt øst-vest, eller nord-syd kommer vi tilbake til utgangspunktet på både en torus eller klode.
En sylinder har to kanter.
En hyperkube er en firedimensjonal analog til kuben, og består av 8 kuber. En firedimensjonal hypersfære består av en sekvens av sfærer.
Den amerikanske matematikeren Dennis Parnell Sullivan fikk Abelprisen 2022 «for hans grunnleggende bidrag til topologi i bredeste forstand, og spesielt for algebraiske, geometriske og dynamiske aspekter». Sullivan har også arbeidet med kaosteori hvor integrallinjer kan danne topologiskemønstre.
Fotballmolekyl
Et ”fotballmolekyl” er et karbon-60 (C-60) molekyl (fullerener, etter Buckminster Fuller) som består av 12 pentagoner (5 sider og hjørner) og 20 heksagoner (6 sider og hjørner). Totalantall sider og hjørner blir 12∙5 + 20∙6 = 180 hjørner og sider. Tre av sidene møtes i hvert hjørne 180/3= 60 hjørner. To av sidene i hhv. pentagoner og heksagoner møtes i hver sidekant 180/2= 90 kanter. Dette tilsvarer 60 karbonatomer (C) og 90 bindinger mellom C-atomene.
Escher-symmetrier
Eksempler på Escher-symmetrier og Möbius-bånd, også med tesselering.

Escher har også laget flere grafiske framstillinger som gir en logisk brist i vår hjerne, hvor det for eksempel ser ut som vannet renner oppover. Escher, M.C. & Locher, J.L.: The infinite world of M.C.Escher. Abradale Press 1984.

Maurtis Cornelis Escher (1898-1972) studerte symmetrier i mosaikk i kirker og moskeer, og laget selv mosaikker bestående av fisk, fugler og øgler. Han var inspirert av den ungarske matematikeren George Pòlya (1887-1985) som fant at det er bare mulig å lage 17 forskjellige symmetrier (Über die Analogie der Krystallsymmetrie in der Ebene (Zeitschrift für Krüstallographie (1924)). Røntgendiffraksjon gir et mål på symmetri i krystaller.

Möbiusbånd
Et Möbiusbånd har bare en kant og er en flate som ser ut som bare en side. (August Ferdinand Möbius).

Et Möbius-bånd er en ikke-orienterbar flate. To Möbiusbånd limt sammen kant mot kant gir en Kleinflaske. En Klein-flaske (Felix Klein 1849-1925) har en fleksibel hals i flasken som føres tilbake i flasken. Den har således ingen inn- eller utside.
Et Möbius-bånd kan lages ved å klippe ut et papirbånd som skjøtes sammen etter å ha vridd det en gang. Hvis man starter å klippe i båndet ca. 1/3 inn fra kanten gir dette to papirstriper som henger i hverandre, en mindre og en større. Möbiusbåndet har bare en side hvis antall vridninger er oddetall, og to sider hvis antall vridninger er liketall (partall).
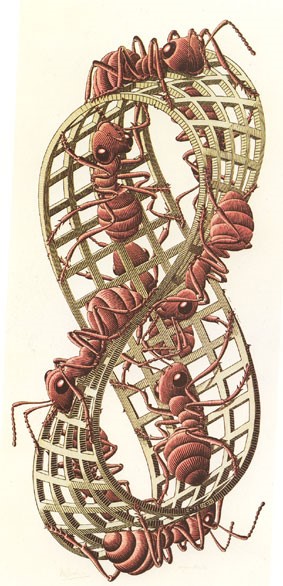
Den nederlandske kunsteren Maurits Cornelis Escher (1898-1972) ga kunstneriske uttrykk av optiske og fysiske umulige konstruksjoner, også tilknyttet uendelighet
Lim sammen en papirstrimmel etter å ha vridd den en gang. Klipp med saks langs båndet og la deg fascinere at båndet har bare en side !

Lag to Möbius-bånd, det ene høyredreiende og det andre venstredreiende. Fest de to båndene i hverandre med 90o vinkel, og klipp opp. Høyre- og venstre-dreiet Möbius-bånd. Fest dem i rett vinkel i hverandre, klipp opp og få følgende:

Du ender med to hjerter, som du kan gi til en du er glad i.
Skal man lage julelenke av farget glanspapir (helst med farge på begge sider av arket), kan man gjøre en vri og lage en lenke av Möbius-bånd i stedet.

Resirkuleringssymbolet for resirkulering av innpakningsmateriale o.a. er konstruert som et Möbiusbånd, vridd to ganger.

Bruene i Königsberg
I Königsberg i Øst-Preussen, nåværende Russland, har elven Pregel to øyer, og er et eksempel på en topologisk problemstilling, studert av Leonhard Euler. Øyene og breddene er forbundet med syv bruer.
Er det mulig å gå en tur, passere hver av de syv bruene bare en gang og returnere til utgangsstedet ?
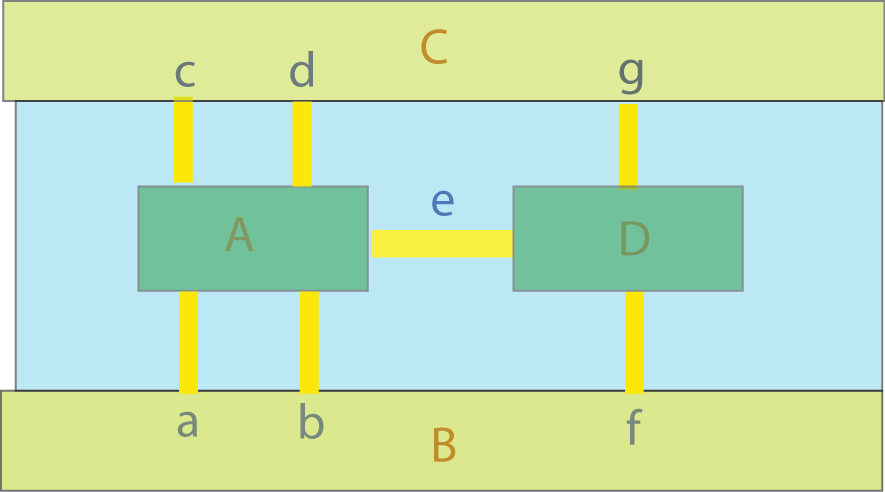
Euler fant løsningen på dette i 1736. Det er umulig.
To øyer A og D forbundet med breddene B og C, og hverandre via 7 bruer a,b,c,d,e,f og g. Et eksempel på grafteori hvor punkter er koblet sammen med linjer.
Skal en Euler-passering av broer være mulig dvs. mulig å passere en bro bare en gang på turen må følgende være oppfylt:
Hvis tallet n, som er antall broer som leder til en region, er et oddetall, så må bokstaver som representerer regioner forekomme ((n+1)/2) ganger.
Hvis tallet n er et partall (liketall), så vil bokstaver som beskriver regionen forekomme n/2 ganger hvis turen starter utenfor regionen og ((n/2) +1) hvis turen starter i regionen.
I Köningsberg er det odde antall broer til hver region, 5,3,3 og 3 til henholdsvis A, B, C og D.
Hvilket betyr at regionene må forekomme 3,2,2,2=9 ganger som er mer enn antall bruer + 1, altså er det umulig å gå en tur og passere hver bro bare en gang.
Eksempler på Euler-broer hvor det er mulig å gå en tur og passere hver bro bare en gang:
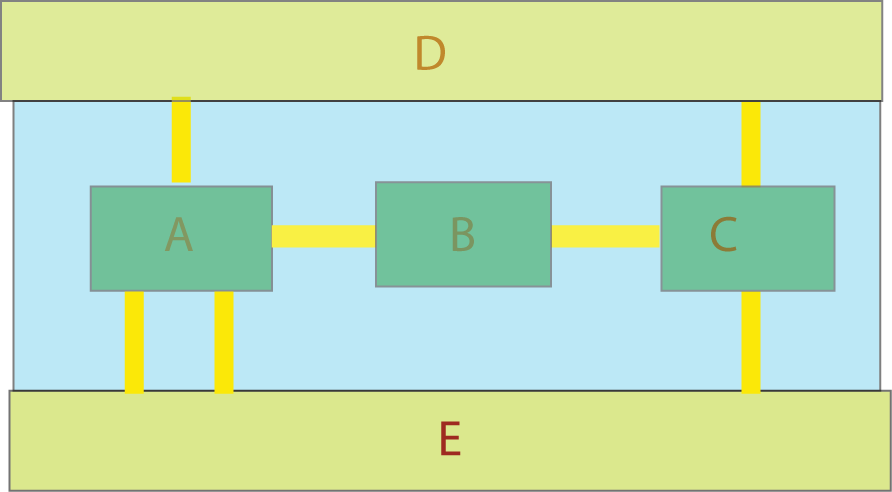
Ifølge Euler-passering av en bro bare en gang er mulig med
EADCBAEC
Til A er det 4 broer (partall) og A er utenfor startregionen da vil A forekomme 4/2=2 ganger. B har to broer (partall)og vil forekomme 2/2=1 ganger. C har tre broer (oddetall) og vil forekomme (3+1)/2= 2 ganger osv.
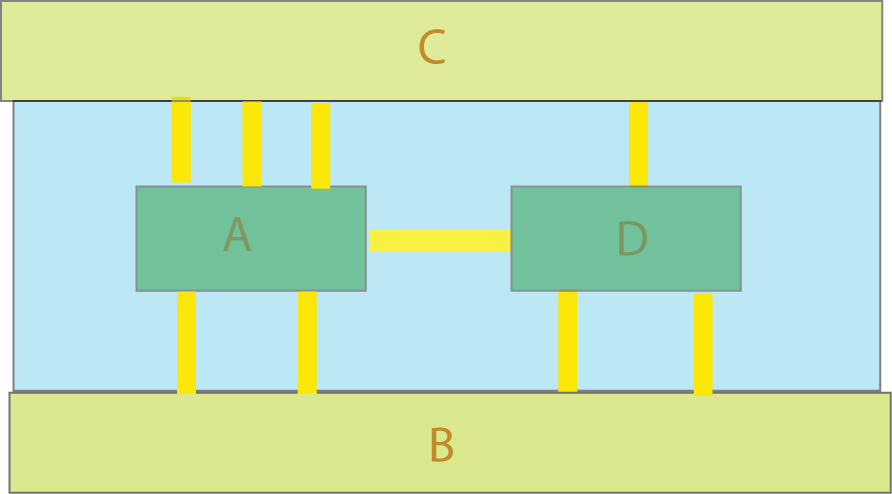
Passering via CBDBADACAC
Hvis det hadde vært fire broer til A så vil A forekomme to ganger hvis turen begynner på utsiden av A og tre ganger hvis den begynner i A.
Tilsvarende eksempler kan finnes i kjemiske synteseveier, gater eller spredningsveier for sykdom.
n-dimensjonale vektorrom
Det Euklidske rom er tredimensjonalt (R3), men det n-dimensjonale vektorrom (Rn) er ikke forskjellig logisk sett.Et rom med n dimensjoner er en manifold. Et punkt har n uavhengige koordinater, og når et punkt beveger seg i rommet er det minst en koordinatt som endrer seg. Guiseppe Peano (1858-1932) laget aksiomer for vektorrom. Peano gjorde bl.a. undersøkelser av en romlig trekant på en kule. (Tegn en trekant på en appelsin og skrell appelsinen). Clas Hugo Herman Weyl (1885-1955) laget aksiomer for rom, stoff og tid.
Ifølge Poincarés konjektur (Jules Henri Poincaré (1854-1912) er kulen en 2-sfære, og en n-sfære er overflaten på et ”n+1-legeme”. Tegner man en lukket løkke på en kule er det mulig å minske løkken uten at den forlater overflaten, til den til slutt ender i et punkt. Kulen er det eneste objekt hvor dette er mulig. På en torus finnes det derimot løkker som ikke lar seg skrumpe til et punkt. Legger man en trådløkke omkring en appelsin kan løkken minskes til et punkt uten å kutte i tråden eller appelsinen. Hvis tråden derimot tres igjennom hullet på en smultring (torus) så kan ikke trådløkken minskes til et punkt. Stephen Smale kunne i 1960 vise at Poincarés konjektur (formodning) gjelder for fem dimensjoner og videre oppover. Den eksentriske russiske matematikeren Grigori Perelman (1966-) beviste Poincarés konjektur i 2002, publisert på internett. Perelman sa nei til både prispenger som var utlovet og Field medaljen.
Apollonius sirkler
Appolonius fra Perga skrev flere bøker om kjeglesnitt, og laget Apollonios problem. Hvor mange sirkler er det mulig å trekke hvor sirkelen skal berøre alle de tre objektene ?
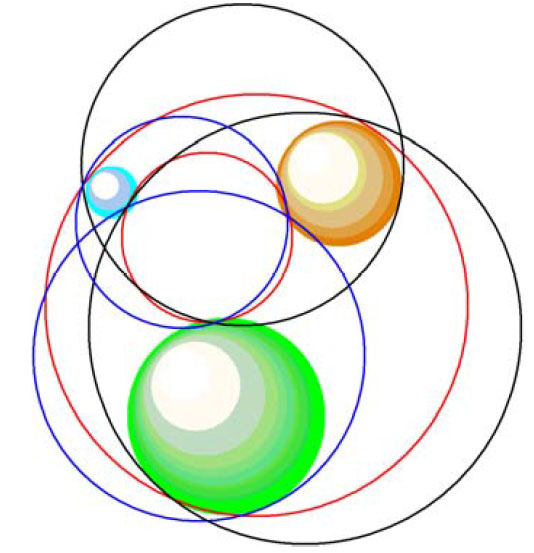
Her er det tegnet opp 6 muligheter, men det er flere.
Knutetopologi
En knute er en lukket løkke med topologi = 0. Ekvivalente knuter kan transformeres til hverandre. Knuteteori og manifoldteori er en del av topologien. Objekter kan bli transformert ved bøyning, vridning, strekning og sammenpressing.
Kjeder og ledd
Et kjede kan lages fra lukkete ledd som hektes sammen, enklest to ringer som henger sammen. Et åpent og lukket perlekjede.
Borromeoringer er tre ringer koblet sammen slik at hektes to av ringene fra hverandre blir automatisk alle tre ringene løse.
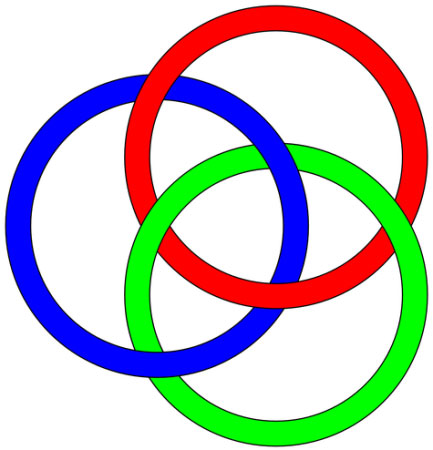
Borromeoringer oppkalt etter Borromeofamilien i Italia som hadde dette i sitt våpenskjold. Løsner en av ringene så løsner de to andre. I et ikosaeder kan man man gjennom hjørnene trekke tre gyldne triangler og disse tre trianglene henger sammen i en form for Borromeoringer.
De olympiske ringer fra 1906 representerer fem kontinenter.
Innen norrøn mytologi kjenner man til tre trekanter lukket i hverandre, en såkalt valknute.
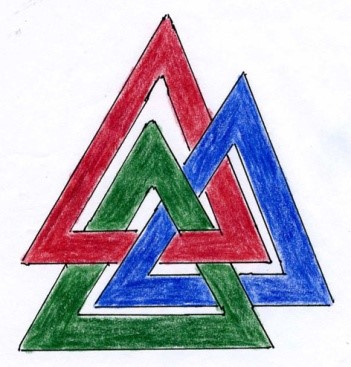
Valknute
Kulepakking
Keplers kulepakkingsproblem, Keplers konjektur (formodning). Hvordan stable kuler av lik størrelse slik at det blir mest mulig kompakt i det Euklidske rom (3D) ? Hver kule omgitt av 6 kuler i et lag. Neste lag slik at kulene faller ned i fordypningen fra første lag. osv. Stabling av appelsiner i fruktdisken. Heksagonal pakking er mest kompakt, ca. 74%
\(\displaystyle\frac{\pi}{\sqrt{18}}=0.7404805...\)
Den norske matematikeren Axel Thue (1863-1922) arbeidet med en todimensjonal analog til Keplers konjektur. Thue arbeidet også med difantiske ligninger, og har fått sitt navn tilknyttet Thue-Morse-sekvens, Thues ligning, Thues teorem, Thue-Siegel-Roth teorem. Hans elev var Thoralf Skolem som arbeidet med mengdelære og matematisk logikk.
Grafteori
Grafteori omhandler noder og koblingslinjer mellom noder. For eksempel firefargeproblemet, Fano-plan og kjemiske bindinger mellom atomer.
Firefargeproblemet, en del av topologien, viser seg at man må benytte fire farger for å fargelegge et kart slik at ingen stater med felles grense har samme farge. Francis Guthrie formulerte problemstillingen i 1852 da han skulle fargelegge et kart over England. Bevist av Kenneth Appel og Wolfgang Hagen i 1976 ved hjelp av et databevis. Det er en nær tilknytning til Graf-teori. Det er umulig for fem land å være plassert slik at hver av dem er i kontakt med de fire andre.
Litteratur
Wikipedia