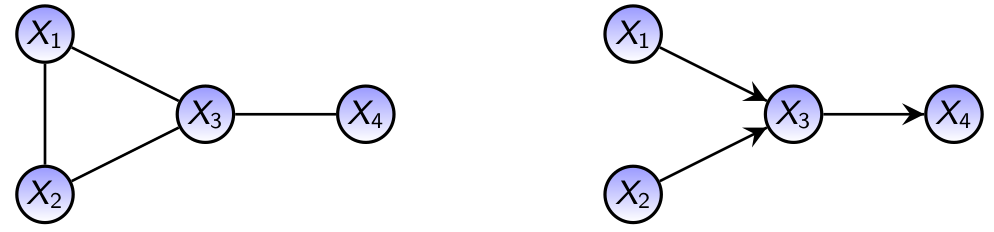
High-dimensional Bayesian estimation of causal effects with directed graphical models (this project will be co-supervised by Vera Kvisgaard)
The aim of this project will be to estimate causal effects from data over a large collection of variables following a multivariate normal distribution. More specifically, the idea is to use Bayesian structure learning for directed graphical models, or causal Bayesian networks, in combination with a causal effect estimation technique known as the backdoor adjustment formula (Pearl, 2009). This approach was developed by Maathuis et al. (2009) in a frequentist setting and later extended to the Bayesian setting by Pensar et al. (2020). The research question of this project will be to investigate if the method by Pensar et al. can improved upon by a more careful selection of adjustment sets in the backdoor formula.
J. Pearl (2009). Causality: Models, Reasoning and Inference. Cambridge University Press.
High-dimensional approximate Bayesian structure learning of undirected graphical models
The aim of this project will be to develop a method for learning the undirected graph structure (or the dependence structure) over a large collection of variables. More specifically, the idea will be to extend the method developed in Pensar et al (2017) into a fully Bayesian setting which will enable computation of (approximate) edge inclusion probabilities, i.e. the probability of there being an edge between two nodes in the graph. A particular focus will be put on scalability, in the sense that the method should be applicable on systems containing at least hundreds of variables.
Generative probabilistic classification with graphical models
Probabilistic classification models for predicting the class of some categorical variable \(Y\) based on some features \(\boldsymbol{X}=(X_1 , \ldots , X_n)\) can be either discriminative or generative. While discriminative model is trained directly on the objective of interest, \(P(Y \mid \boldsymbol{X})\), a generative model focus on the modelling the class-specific distributions of the features \(P(\boldsymbol{X} \mid Y)\) and produce predictions using Bayes' formula, \(P(Y \mid \boldsymbol{X}) \propto P(\boldsymbol{X} \mid Y) P(Y)\). Discriminative models are most often superior in terms predictive accuracy, but not always (See Ng & Jordan, 2001). On the other hand, generative models will possess some advantageous properties when it comes to, for example, uncertainty-awareness and imbalanced class distributions. The aim of this project will be to compare the performance of discriminative models against graphical- model-based generative models in different settings.