Løsningsforslag nr. 1 for MA 001 høsten 2000

Oppgave 1

(a)

Den opprinnelige absolutte temperaturen er T₀ = 20.0 + 273.15 = 293.2 grader Kelvin. Den nye absolutte temperaturen er T₁ = 40.0 + 273.15 = 313.2 grader Kelvin. Vekstfaktoren er T₁/T₀ = 1.0682 = 1 + 6.82/100.

Den prosentvise økningen i absolutt temperatur er derfor 6.82%.

Vekstfaktoren for varmeutstrålingen er lik

P₁/P₀ = (aT₁⁴)/(aT₀⁴) = (T₁/T₀)⁴ = (1.0682)⁴ = 1.302 = 1 + 30.2/100.

Den prosentvise økningen i varmeutstrålingen er derfor 30.2%.

(b)

La T₀ = 293.15 være den opprinnelige temperaturen, og la T være den nye temperaturen, målt i Kelvin. La P₀ = a T₀⁴ være den opprinnelige varmeutstrålingen og la P = a T⁴ være den nye varmeutstrålingen. Da er P = 2 P₀, så

a T⁴ = 2 a T₀⁴,

Legemets nye temperatur er 75.47 °C.

Oppgave 2

(a)

• 2x + 2y <= 360 svarer til betingelse 1.
• 2x + y <= 300 svarer til betingelse 2.
• x + 3y <= 400 svarer til betingelse 3.
• x >= 0 og
• y >= 0 svarer til at det ikke kan lages et negativt antall harde eller myke pakker.

(b)

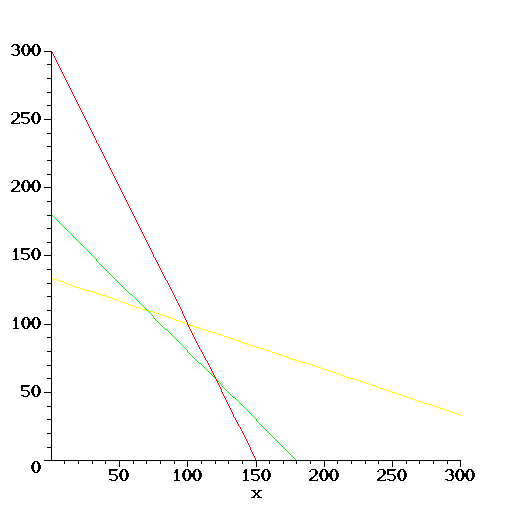
(Området mellom x-aksen, y-aksen og de tre hellende linjene skraveres.)

Det øvre venstre hjørnet er bestemt av likningene 2x+2y=360 og x+3y=400. Den første likningen kan skrives x+y=180. Ved subtraksjon fås 2y = (x+3y)-(x+y) = 400-180=220, så y=110. Innsatt i x+y=180 gir dette x=70. Alternativt kan x=70 settes inn i de to likningene, som så begge gir at y=110.

Det nedre høyre hjørnet er bestemt av likningene 2x+2y=360 og 2x+y=300. Ved subtraksjon fås y = (2x+2y)-(2x+y) = 360-300 = 60. Innsatt i 2x+y = 300 gir dette x = (300-60)/2 = 120. Alternativt kan x=120 settes inn i de to likningene, som så begge gir at y= 60.

Områdets to hjørner i 1. kvadrant har xy-koordinater (70, 110) og (120, 60).

(c)

Vi finner først resten av områdets hjørner.

Hjørnet på x-aksen er bestemt av y=0 og 2x+y=300, som gir x=150. Hjørnet er (150, 0).

Hjørnet på y-aksen er bestemt av x=0 og x+3y=400, som gir y=400/3 (= 133.3). Hjørnet er (0, 400/3).

Det siste hjørnet er origo, (0, 0).

Vi beregner funksjonsverdien f(x, y) = x + 2y i de 5 hjørnene:

• f(70, 110) = 70 + 2 x 110 = 290.
• f(120, 60) = 120 + 2 x 60 = 240.
• f(150, 0) = 150 + 2 x 0 = 150.
• f(0, 400/3) = 0 + 2 x 400/3 = 800/3 (= 266.7).
• f(0, 0) = 0 + 2 x 0 = 0.

Den største verdien finnes i (x, y) = (70, 110). Den antatte mottakergleden f er størst hvis det leveres 70 harde og 110 myke pakker.

(d)

Vi beregner funksjonsverdien g(x, y) = 1.4x + 1.2y i de 5 hjørnene:

• g(70, 110) = 1.4 x 70 + 1.2 x 110 = 230.
• g(120, 60) = 1.4 x 120 + 1.2 x 60 = 240.
• g(150, 0) = 1.4 x 150 + 1.2 x 0 = 210.
• g(0, 400/3) = 1.4 x 0 + 1.2 x 400/3 = 160.
• g(0, 0) = 1.4 x 0 + 1.2 x 0 = 0.

Den største verdien finnes i (x, y) = (120, 60). Den justerte mottakergleden g er størst hvis det leveres 120 harde og 60 myke pakker.

Oppgave 3

(a)

f₀(x) = 4 cos(x) + 3 cos(x) = 7 cos(x) har middelverdi 0, amplitude 7, periode 2 og akrofase 0.

(b)

f_/2(x) = 4 cos(x) + 3 cos(x - /2) = 4 cos(x) + 3 sin(x) = C cos(x - x₀) der C² = 4² + 3² = 16 + 9 = 25, så C = 5, og tan(x₀) = 3/4 mens x₀ ligger i 1. kvadrant, så x₀ = tan^-1(3/4). Altså har f_/2(x) middelverdi 0, amplitude 5, periode 2 og akrofase tan^-1(3/4) = 0.6435 radianer = 36.87 °.

(c)

f(x) = 4 cos(x) + 3 cos(x - ) = 4 cos(x) - 3 cos(x) = cos(x) har middelverdi 0, amplitude 1, periode 2 og akrofase 0.

(d)

(e)

f_t(x) = 4 cos(x) + 3 cos(x-t) = (4 + 3 cos(t)) cos(x) + 3 sin(t) sin(x) = C cos(x - x₀) har akrofase x₀ gitt ved tan(x₀) = 3 sin(t) / (4 + 3 cos(t)) . Akrofasen ligger i 1. kvadrant fordi (4 + 3 cos(t)) og 3 sin(t) er positive for 0 < t < . Siden tan er strengt voksende er x₀ størst der hvor tan(x₀) er størst, dvs. der hvor 3 sin(t) / (4 + 3 cos(t)) er størst.