Eksponentialfordelingen angir tiden det tar før en hendelse skjer, hvor hendelsen skjer med konstant sannsynlighet per tidsenhet. Hvis vi sammenligner med den geometriske fordelingen som er diskret så er eksponentialfordelingen den tilsvarende kontinuerlige utgaven. Den er også lik gammafordelingen med formparameter lik 1. Eksponentialfordeling av stokastiske variable har likhetstrekk med Poisson-fordeling. Standardavviket er lik gjennomsnittet.
Sannsynlighetstetthetsfunksjonen for eksponentialfordelingen f(x) er:
\(f(x)= \displaystyle\lambda e^{-\lambda x}\;\;\;\;\;\; x \geq0\)
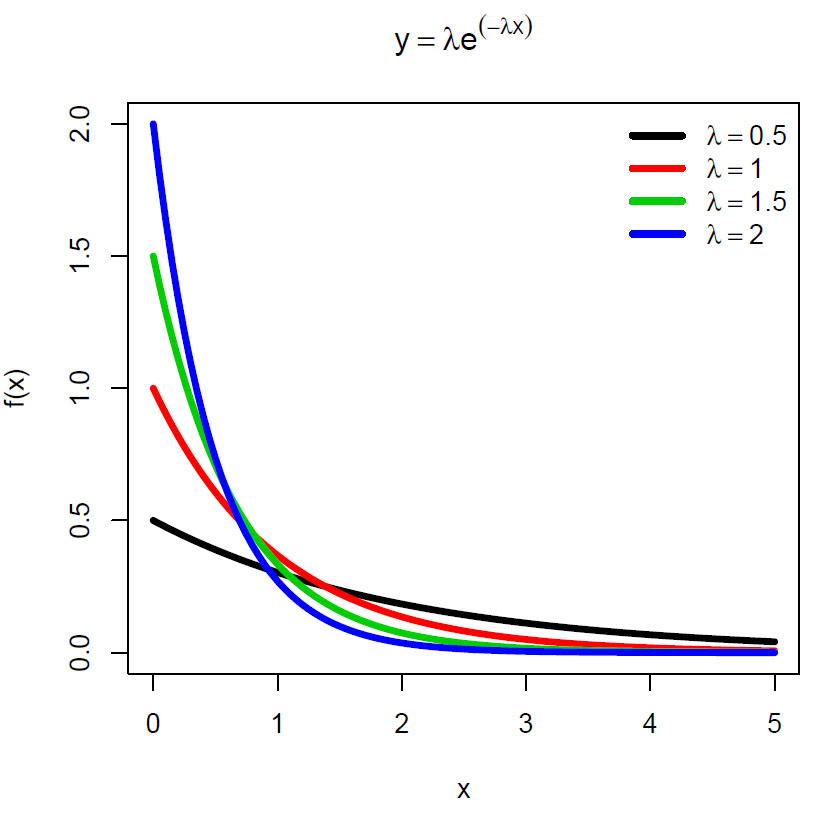
Sannsynlighetstetthetsfunksjonen for eksponentialfordelingen for forskjellige verdier av lambda (λ). Arealet under en sannsynlighetstetthetsfunksjon er lik 1 integrert over hele sannsynlighetsområde.
For en gitt positiv konstant λ og en tilfeldig variabel X bli den kumulative sannsynligheten, fordelingsfunksjon F(x) for eksponentialfordelingen:
\(F(x)=\displaystyle 1- e^{-\lambda x}\;\;\;\;\;\; \text{for }\; x \geq\; 0\)
\(F(x)= 0 \;\;\; \text{for}\; x<0\)
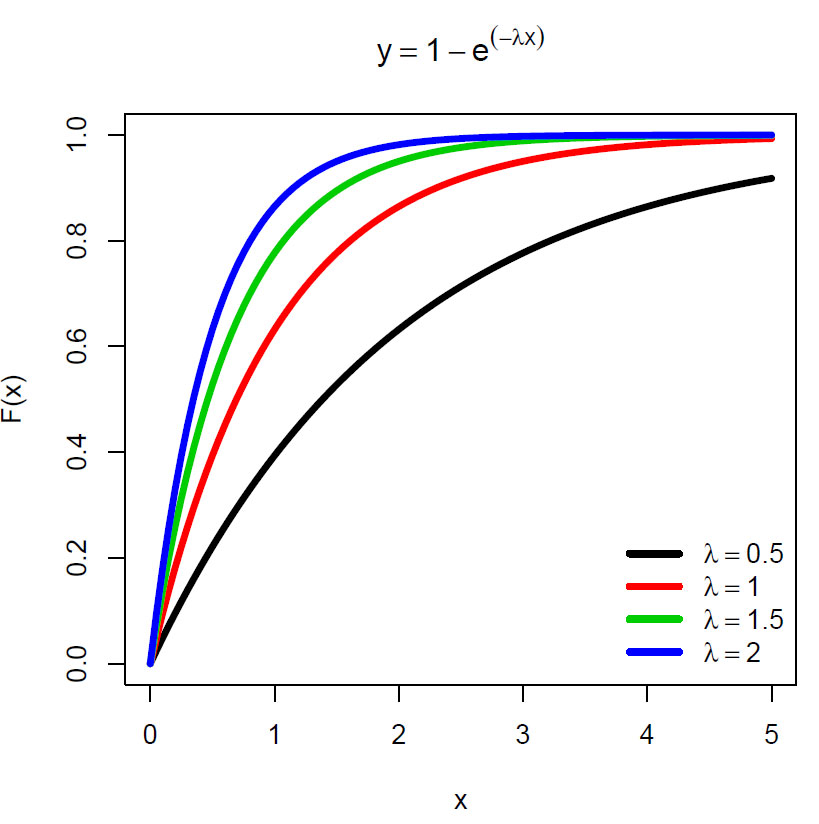
Den kumulative sannsynlighetsfunksjonen F(x) for eksponentialfordelingen for for forskjellige verdier av lambda (λ).
Forventing E(X), varians Var(X) g variasjonskoeffisient CV for eksponentialfordlingen er:
\(E(X)=\displaystyle \frac{1}{\lambda}\;\;\;\;\;\;\; Var(X)= \frac{1}{\lambda ^2}\;\;\;\;\;\;\; CV=1\)
\(E(X)= \displaystyle\lambda \int_0 ^\infty x\; \lambda e^{-\lambda x}= \frac{1}{\lambda}\)
Gammafordelingen hvor formparameter alfa (α)=1 tilsvarer en eksponentialfordeling:
\(f(x)=\displaystyle \frac {1}{\beta}e ^ {\frac{-x}{\beta}}\;\;\;\;\; x>0\)
I eksponentialfordelingen bruker man ofte hastighetsparameter lambda (λ) hvor λ=1/β.
Sannsynligheten går mot 0 når x→-∞ og mot 1 når x→-∞. Desintegrering av atomer av en radioaktiv isotop er en tilfeldig hendelse og følger en Poisson-fordeling. Vi kan også se på dette via eksponentialfordelingen. Desintegreringen følger differensialligningen for endringen i antall atomer N per tidsenhet:
\(\displaystyle\frac{dN}{dt}= -kN\)
hvor k er nedbrytningskonstanten. Differentialligningen har den analytiske løsningen:
\(N= \displaystyle N_0 e^{-kt}\)
hvor N0 er antall radioaktive atomer når t=0. Sannsynligheten for at et atom vil desintegrere ved tiden t er:
\(\displaystyle\frac{N_0 - N}{N_0}= 1- e^{-kt}\)
det vil si fraksjonen av den opprinnelige mengden som desintegrerer ved tiden t.