De første Bernoulli-tallene er,
B0 1
B1 -1/2
B2 1/6
B4 -1/30
B6 1/42
B8 -1/30
B10 5/66
B12 -691/2730
B14 7/6
B16 -3617/510
og bortsett for B1 så er alle
\(B_{2k+1}=0\)
Det vil si B3=B5= 0 osv.
Bernoulli-tallene Bn kan beskrives som en Taylor-rekke:
\(\displaystyle\frac{x}{e^x-1}=\sum_{n=0}^\infty B_n \frac{x^n}{n!}\)
Denne funksjonen har poler ved 2πn slik at |x|<2π
Figur
\(\displaystyle\frac{x}{2}+\frac{x}{e^x -1}=\frac{x}{2}\frac{e^x + 1}{e^x - 1}= \frac{x}{2}\cot\frac{x}{2}\)
Rekurrensformelen blir:
\(\displaystyle\frac{x}{e^x-1}e^x=x+ \frac{x}{e^x-1}\)
Bernoulli-tall finnes igjen om koeffisienter i Taylorutvikling av følgende:
\(\displaystyle\frac{x}{1-e^{-x}}\)
\(\displaystyle\frac{1}{2}\cot\left(\frac{1}{2}x\right)\)
Venstre side av den ligningen kan uttrykkes som et produkt av potensrekker:
\(\displaystyle\left(\sum_{n=0}^\infty B_n \frac{x^n}{n!}\right) \left(\sum_{m=0}^\infty \frac{x^m}{m!}\right)= x + \sum_{n=0}^\infty B_n \frac{x^n}{n!}\)
Vi kan sammenligne koeffisienten for xn på begge sider:
\(\displaystyle\frac{B_n}{n!}= \sum_{k=0}^n \frac{B_k}{k!(n-k)!}\)
Bernoulli-tallene kan man også finne igjen i rekkeutvikling av tan(x), x/sin(x), og log(sin(x)/x).
Det er en sammenheng mellom Bernoulli-tall, primtall og Riemanns zetafunksjon ζ(s) hvor s er et komplekst tall z=a+bi
\(\zeta(s)=\displaystyle\sum_{n=1}^\infty \frac{1}{n^s}= \frac{1}{1^s}+ \frac{1}{2^s}+ \frac{1}{3^s}+\dots\)
Rekken konvergerer for alle komplekse tall s som har reell del >1.
Euler fant en sammenheng mellom zetafunksjonen og primtall for s=1, videre bevist i 1876 av Leopold Kronecker (1823-1891) hvor p er et primtall
\(\zeta(s)=\displaystyle\sum_{n=1}^\infty \frac{1}{n^s}=\prod_p^\infty\frac{1}{1-\frac{1}{p^s}}\)
Euler fant også Bernoulli-tall i løsningen av Basel-problemet som var å finne grenseverdien for følgende rekke, første gang formulert av Jakob Bernoulli, for zetafunksjonen (2):
\(\zeta(2)=\displaystyle\sum_ {k=1}^\infty \frac{1}{k^2}= \frac{\pi^2}{6}\)
ζ(3) gir et irrasjonalt tall (Apérys konstant) 1.202057...
Seinere fant man at følgende rekker konvergerte:
\(\zeta(4)= \frac{\pi^4}{90}\)
\(\zeta(6)= \frac{\pi^6}{945}\)
\(\zeta(8)= \frac{\pi^8}{9450}\)
Eller mer generelt, for positive liketall av typen 2n inngår Bernoulli-tallet for 2n (B2n):
\(\zeta(2n)= \displaystyle\frac{(-1)^{n-1}2^{2n-1}B_{2n}}{(2n)!}\pi^{2n}\)
Som også kan skrives som:
\(\displaystyle\sum_{k=1}^\infty \frac{1}{k^n}= \frac{2^n|B_n|\pi^n}{2(n!)}\)
Det er også sammenheng mellom Bernoulli-tall og Euler-Mascheroni konstant gamma
\(\gamma=\displaystyle\frac{1}{2} \sum_{k=1}^\infty \frac{B_{2k}}{2k}\)
Vi kan snu på ligningen og bruke den til å finne verdien for Bernoullitall av typen 2k:
\(|B_n|=\displaystyle\frac{2(2k)!}{(2\pi)^{2k}}\zeta(2k)\)
n fakultet (n!) stiger raskt med økende n, men vi kan da forenkle ved å bruke Stirlings formel, (James Stirling (1692-1770).
\(n!\approx\sqrt{2\pi n}\left(\frac{n}{e}\right)^n \approx \sqrt{2\pi} \cdot e^{-n}\cdot n ^{n+\frac{1}{2}}\)
Dessuten blir ζ(2k)≈1
Pentagonale og heksagonale tall
Dette er tall som man finner igjen som punkter langs sidene på henholdsvis pentagon og heksagon.Pentagonale tall (pn) følger formelen:
\(p_n= \displaystyle\frac{n(3n-1)}{2}\)
De 20 første pentagonale tall
1 5 12 22 35 51 70 92 117 145 176 210 247 287 330 376 425 477 532 590
Heksagonale tall hn følger formelen:
\(h_n= \displaystyle\frac{2n(n-1)}{2}\)
De 20 første heksagonale tall:
1 6 15 28 45 66 91 120 153 190 231 276 325 378 435 496 561 630 703 780
Eulertall
Eulertall En er av type:
\(\displaystyle\frac{1}{\cosh (x)}= \frac{2}{e^x+ e^{-x}}= \sum_{n=0}^\infty \frac{E_n}{n!}x^n\)
hvor cosh er hyperbolsk cosinus.
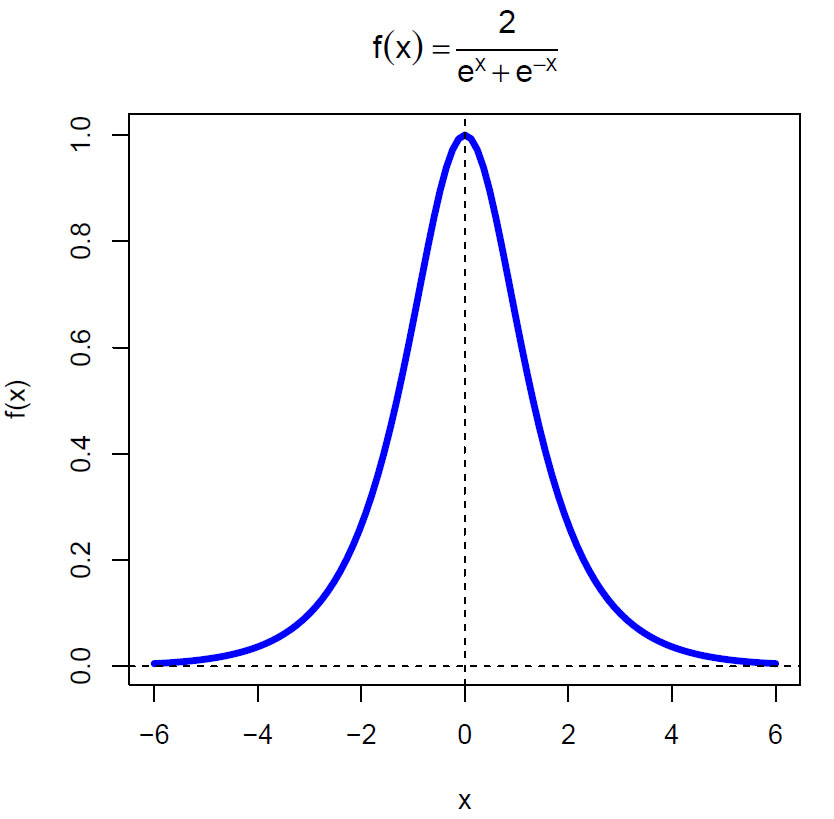
De odde-indekserte Eulertallene er alle lik 0, mens de andre Eulertallene er en sekvens av heltall:
Eo 1
E2 -1
E4 5
E6 -6
E8 1385
E10 -50521