Største felles divisor eller største felles faktor for to eller flere heltall, er det største tallet som deler tallene uten at det blir noen rest. Største felles divisor for a=8 og b=12 er lik 4. a og b kalles koprimtall hvis det eneste positive heltallet som deler begge av dem er lik 1. Det vil si at største felles divisor er lik 1.
Phifunksjonen teller antall positive heltall mindre eller lik n som er relative primtall til n.
\(\phi (n)= n \displaystyle \prod{_{p|n} }\left(1- \frac{1}{p}\right)\)
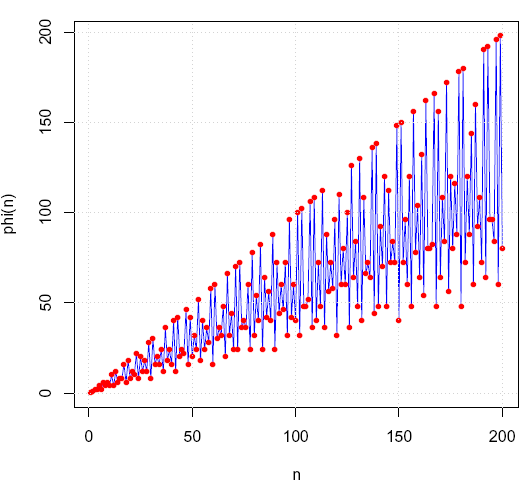
Eulers phi-funksjon for n=0-200
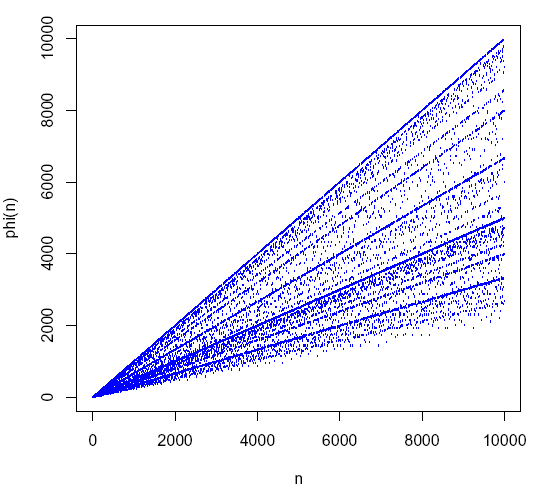
Eulers phi-funksjon for n=0-10000.
|
n φ(n) 1 0 2 1 3 2 4 2 5 4 6 2 7 6 8 4 9 6 10 4 11 10 12 4 13 12 14 6 15 8 16 8 17 16 18 6 19 18 20 8
|
n φ(n) 21 12 22 10 23 22 24 8 25 20 26 12 27 18 28 12 29 28 30 8 31 30 32 16 33 20 34 16 35 24 36 12 37 36 38 18 39 24 40 16
|
n φ(n) 41 40 42 12 43 42 44 20 45 24 46 22 47 46 48 16 49 42 50 20 51 32 52 24 53 52 54 18 55 40 56 24 57 36 58 28 59 58 60 16
|
n φ(n) 61 60 62 30 63 36 64 32 65 48 66 20 67 66 68 32 69 44 70 24 71 70 72 24 73 72 74 36 75 40 76 36 77 60 78 24 79 78 80 32
|
n φ(n) 81 54 82 40 83 82 84 24 85 64 86 42 87 56 88 40 89 88 90 24 91 72 92 44 93 60 94 46 95 72 96 32 97 96 98 42 99 60 100 40 |
De 100 første φ(n)
Eulers phi-funksjon kan anvendes innen kryptografi. Man finner to ekstremt store primtall p og q, og renger ut n=pq og k=φ (n). Deretter finner man to tall e og d slik at
\(ed \equiv 1(\bmod (p-1)(q-1))\)
n og k er offentlige nøkler og d er privat dekrypteringsnøkkel.
Vi viser prinsippet for RSA med noen meget små primtall:
p=13 og q=17, samt k=7, n=187, φ(n)=160, d=23
Bokstaven A i ASCII tilsvarer desimaltall 65. Etter koding blir denne til tallet 91, tilsvarende venstre klammeparentes [ i ASCII.
Skal man dechiffrere må man regne ut den private nøkkel d med Euklids algoritme:
\(kd \equiv 1(\bmod (p-1)(q-1))\)
Dvs. d=23
Vi kommer nå tilbake til M ved:
\(M \equiv 11^{23}(\bmod 187) \)
Dette blir litt for store tall å hanskes med så vi kan bruke Kinesisk restteorem for å øke hastigheten for denne utregningen.
φ(n) er multiplikativ så hvis to primtall m og n er relative primtall i forhold til hverandre så vil:
\(gfd(m, n)=1 \;\;\;\implies \;\; \phi(m,n)=\phi(m)\phi(n)\)
Flere egenskaper gjelder hvis a og b er koprimtall. Ikke noe primtall kan dele både a og b.
Det eksisterer heltall x og y slik at (Bézouts identitet):
\(ax + by=1\)
Heltallet b er en multiplikativ invers modulo a, det vil si at det finnes et heltall y sli at:
\(by\equiv 1(\bmod a)\)
\(\phi(p) ^k=p^k - p^{k-1}=p^{k-1}(p-1)=p^k \left(1-\frac{1}{p}\right)\)
Hvis vi har to heltall a og b, hva er sannsynligheten for at de er koprimtall ? Sannsynligheten for at et tall er delelig med et primtall p er lik 1/p, for eksempel er hvert 11te heltall delelig med 11. Sannsynligheten for at både a og b er delelig med et primtall blir 1/p2, og sannsynligheten for at minst en av dem ikke er delelig med et primtall er 1-1/p2. Som produkt over alle primtall gir dette en ca. sannsynlighet 61%
\(\displaystyle\prod _p ^\infty \left(1-\frac{1}{p^2}\right)=\left(\prod _p ^\infty \left(1-\frac{1}{p^2}\right)\right)^{-1}=\frac{1}{\zeta(2)}=\frac{6}{\pi ^2}\)
Carmichaels lambdafunksjon λ(n) til et positivt heltall n er det minste positive heltallet m for hvert heltall a som er koprimtall til n:
\(a^m \equiv 1(\bmod n)\)
λ(n)= φ(n) hvis n=2,3,4,5,7,9,11,13,17,19,23,25…
λ(n)= ½ φ(n) hvis n=8,16,32,64,…
En primtallstest er en algoritme som avgjør om et tall sannsynligvis er et primtall eller ikke, testene gir vanligvis bare indikasjoner. Fermats primtallstest er en slik enkel test: gitt et heltall n, finn et heltalls koprimtall a og beregn
an-1 (modulo n). Hvis dette blir lik 1, er det mulighet for at man har et primtall. an-1 (modulo n)=1, men n ikke er et primtall så kalles n et pseudoprimtall med basis a.
Seinere fant man at Fermats lille teorem kan benyttes til primtallstesting. AKS primtallstesten er en polynomtid algoritme, type P.
Eksponensiering ved kvadrering er en metode får å øke hastigheten når man har potenser med store heltall. Hvis n er et positivt heltall så gjelder, øverst for n er oddetall, nederst for n er liketall:
\( x^n = \begin{cases} x(x^2)^{\frac{n-1}{2}} & \quad \text{hvis } \text{ n er oddetall} \\ (x^2) ^{\frac{n}{2}} & \quad \text{hvis } \text{ n er liketall} \ \end{cases} \)
Dirichlets etafunksjon
Dirichlets etafunksjon, eta(η), også kalt den alternerende zetafunksjon, er en Dirichletserie som konvergerer for alle komplekse tall med reell del >0
\(\eta(s)=\displaystyle\sum_{n=1}^\infty \frac{(-1)^{n-1}}{n^s}=\frac{1}{1^s}-\frac{1}{2^s}+\frac{1}{3^s}-\frac{1}{4^s}+\dots\)
Andre fremstillinger av Dirichlets etafunksjon er, med zeta(s) ζ(s) eller med gamma:
\(\eta(s)=(1-2^{1-s})\zeta(s)\)
\(\eta(s)=\displaystyle\frac{1}{\gamma(s)}\int_0^\infty \frac{x^{s-1}}{e^x + 1}dx\)
Noen utvalgte verdier av Dirichlets etafunksjon:
\(\eta(1)=\ln 2 \;\;\;\;\eta(2)=\frac{\pi^2}{12}\;\;\;\;\eta(4)=\frac{7 \pi^4}{720} \;\;\;\;\eta(6)=\frac{31 \pi^6}{302402}\)
For et heltall k>1 og Bk er det k-te Bernoulli-tall:
\(\eta(1-k)=\frac{2^k-1}{k}B_k\)