Definisjonen av logaritmer med grunntall b (logb) for et tall x er lik y, er slik at grunntallet opphøyd i y er lik x:
\(\log_b x= y \;\;\;\; \; \iff \;\;\; b^y = x\)
Briggske logaritmer
Briggske logaritmer er praktiske hvor tallet x endrer seg i mange tierpotenser (dekader), enten større enn null eller mindre enn null. Det betyr at en tallinje med stort spenn i tall, e.g. tallene fra 1 til en milliard 101 - 109 omdannes til tallene 1-9 skrevet som Briggske logaritmer på x-aksen med en logaritmeskala. Eller tallene for lengde en nanometer (nm) til 1 meter , 10-9 - 100 får tallene -9 - 0 på x-aksen skrevet som Briggske logaritmer. På pH skalaen er H+-konsentrasjonen ved pH=7 lik 10-7 molar (M), men ved å bruke minus konsentrasjonen til H+-konsentrasjonen så snur fortegnet og vi har en skala som går fra pH 0-14, for H+-konsentrasjoner fra meget srut, 100 =1 molar (M) til 10-14 molar (M), meget basisk.
\(pH= -log_{10}\left[H^+\right]\;\;\;\;\;\;\;\; [H^+][OH^-]= 10^{-14}\)
dvs. hvis pH=7 er [H+]=[OH-]=10-7 M
\(10^{\log x}= x \;\;\;\;\; \implies 10^{\log (7)}= 7\)
Analogt for decibelskala for lydtrykk, og Richters skala for jordskjelv, for hvert hele tall i økning på skalalen er det egentlig en ti gangers økning i mengde. Desibel-skalaen for lydtrykk, pH-skalaen for surhet og Richerts skala for jordskjelvbevegelser er eksempler på logaritmiske skalaer. med grunntall 10, altså Briggske logaritmer.
For eksempel med grunntall b=10 (Briggske logaritmer) og tallet x=10000 blir logaritmen til 10000 lik 4:
\(\log_ {10}10000= 4 \;\;\;\; \; \iff \;\;\; 10^4 = 10000\)
Logaritmen til en er lik null:
\(\log_ {10}1= 0 \;\;\;\; \; \iff \;\;\; 10^0 = 1\)
Logaritmen til 10 er lik 1:
\(\log_ {10}10= 1 \;\;\;\; \; \iff \;\;\; 10^1 = 10\)
Logaritmen til 100 er lik 2:
\(\log_ {10}100= 2 \;\;\;\; \; \iff \;\;\; 10^2 = 100\)
Logaritmen til 1000 er lik 3:
\(\log_ {10}1000= 3 \;\;\;\; \; \iff \;\;\; 10^3 = 1000\)
Logaritmen til 0.1 er lik -1:
\(\log_ {10}0.1= 0.1\;\;\;\; \; \iff \;\;\; 10^{-1} =\frac{1}{10}=0.1\)
Hva er logartimen til null (0) ? Jo den er minus uendelig, og lite anvendelig.
\(\log_ {10}0= -\infty\;\;\;\; \; \iff \;\;\; 10^{-\infty}=\frac{1}{10^\infty}= 0\)
Vi kan ikke ta logaritmen til negative tall, slik at x må være større enn 0 (x>0).

Logaritmefunksjonen log10(x). Legg merke til at funksjonen krysser x-aksen ved x=1. Ved x=0 forsvinner funksjonen nedover og nærmer seg asymptotisk mot minus uendelig. Ved økende verdier for x så flater funksjonen av.

Logaritmefunksjonen Briggske logaritmer log10(x) for økende verdier av x. Se at for x=1000 blir log10(1000)= 3.
Naturlige logaritmer
Naturlige logartimer loge(x), og skrives ofte ln(x) har grunntall e. Tallet e, Eulers tall, inngår i eksponentialfunksjonen, og logartimefunksjonen og eksponetialfunksjonen er inverse funksjoner, slik som vist på figuren hvor de er speilvendt rundt aksen x=y
\(\ln x= \log_e x= y \;\;\;\; \; \iff \;\;\; e^y = x\)

Figuren viser eksponentialfunksjonen y=ex, logartimefunksjonen y=ln(x) med grunntall e, samt den rette linjen som går gjennom origo, y=x, i vinkel 45o, og stigningskoeffisient lik 1. Legg merke til at logartimefunksjonen krysser x-aksen ved x=1, ln(1)= 0, og se at eksponentialfunksjonen skjærer y-kasen ved x=0, eo=1. Se også log10(10)= 1 mens loge(10)= 2.302585.
Legg merke til at logartimefunksjonen for naturlige logaritmer og eksponentialfunksjonen speiler seg omkring midtlinjen, de er inverse funksjoner. Eksponentialfunksjonen beskriver eksponentiell vekst og stiger meget raskt (og skremmende) for økende verdier av x.
I statistiske modeller hvor man bruker logartimen til odds, må man bruke eksponentialfunksjonen for å kunne omregne til sannsynligheter.

Briggske logartimer (log(x)) med grunntall 10 (log10(x)) og naturlige (ln(x) logaritmer med grunntall e (loge(x)).

Funksjonen for naturlige logartimer ln(x) med grunntall e. Vi ser, likt med Briggske logaritmer at i logartimefunksjonen med grunntall e er logartimen til 1 lik 0 og logaritmen til 0 er lik minus uendelig (-∞).
\(\lim\limits_{x \to 0+} \ln(x)= -\infty\;\;\;\;\;\;\;\;\;\lim\limits_{x \to \infty} \ln(x)= \infty\)
Vi finner den førstederiverte til logartimefunksjonen:
\(\displaystyle\frac{1}{x}\)
Regneregnler for logaritmer
Siden logartimeregning omhandler potensregning, et grunntall og en eksponent så kan det være lurt å repetere noen regneregler for potensregning, før vi går over til regnereglene for logaritmer
\(b^2 \cdot b^3= (b\cdot b)(b\cdot b \cdot b)= b^{2+3}= b^5\)
\(\left(b^2\right)^3= (b \cdot b)(b \cdot b)(b \cdot b )= b^{2 \cdot 3}= b^6\)
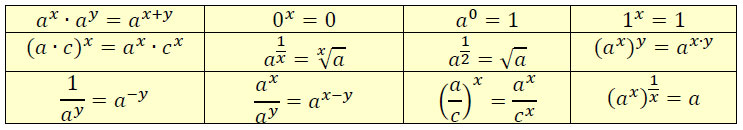
For naturlige logarritmer gjelder, og samme regler gjelder for Briggske logaritmer med grunntall 10.)
\(\ln(x \cdot y)= \ln(x) + \ln(y)\)
\(\ln \left(\displaystyle\frac{x}{y}\right)= \ln(x)-\ln(y)\)
\(\ln \left(\displaystyle\frac{1}{x}\right)= -\ln(x)\)
\(\ln\left(a^x\right)= x \cdot ln(a)\)
\(\ln\left(x^r\right)= r\cdot ln(x)\)
Johan Napier og logaritmer
På 1600-tallet ble det nødvendig å gjøre mer nøyaktige beregninger innen astronomi og navigasjon. Det gjaldt å finne en metode for å redusere arbeidet med multiplikasjoner og divisjoner med tall med mange siffer og desimaler.
John Napier (1550-1617) innførte logaritmer med verket Mirifici logarithmorum canonis descripto (En beskrivelse av den fantastiske regelen til logaritmer) (1614).
Selv om det var Napier som kom på idéen med logaritmer, så var det var Henry Brigg (1561-1631) som konstruerte de første brukbare logaritmetabeller basert på grunntallet 10. Etter diskusjon med Napier kunne Henry Briggs i 1624 publisere en forbedret logaritmetabell basert på grunntallet 10 i Arithmetica logarithmica.
Logaritmer med grunntall 10 (log10) kalles Briggske logaritmer. Briggs måtte for hånd regne ut tallene i logartimetabellene. Når vi skal finne logaritmen til et tall slår vi det bare inn på lommekalkulatoren, men slik var det ikke før. Logaritmetabeller forenklet all multiplikasjon og divisjon til addisjon og subtraksjon, og gjorde spesielt astronomiske beregninger mye enklere.
Her er noen tall, vi ser at logartimen blir halvparten for hver gang og vi har klart å finne logartimen til noen utvalgte tall, så er det bare å fylle ut resten, og husk utregningene ble gjort for hånd.

Regnestaven
Regnestaven var et annet hjelpemiddel, utviklet av matematikeren Edmund Gunter. Regnestaven har to logaritmiske akser som kan forskyves i forhold til hverandre, og en skala til bruk for utregning av kvadratrøtter og kvadrering av tall. Brukt i multiplikasjon og divisjon.
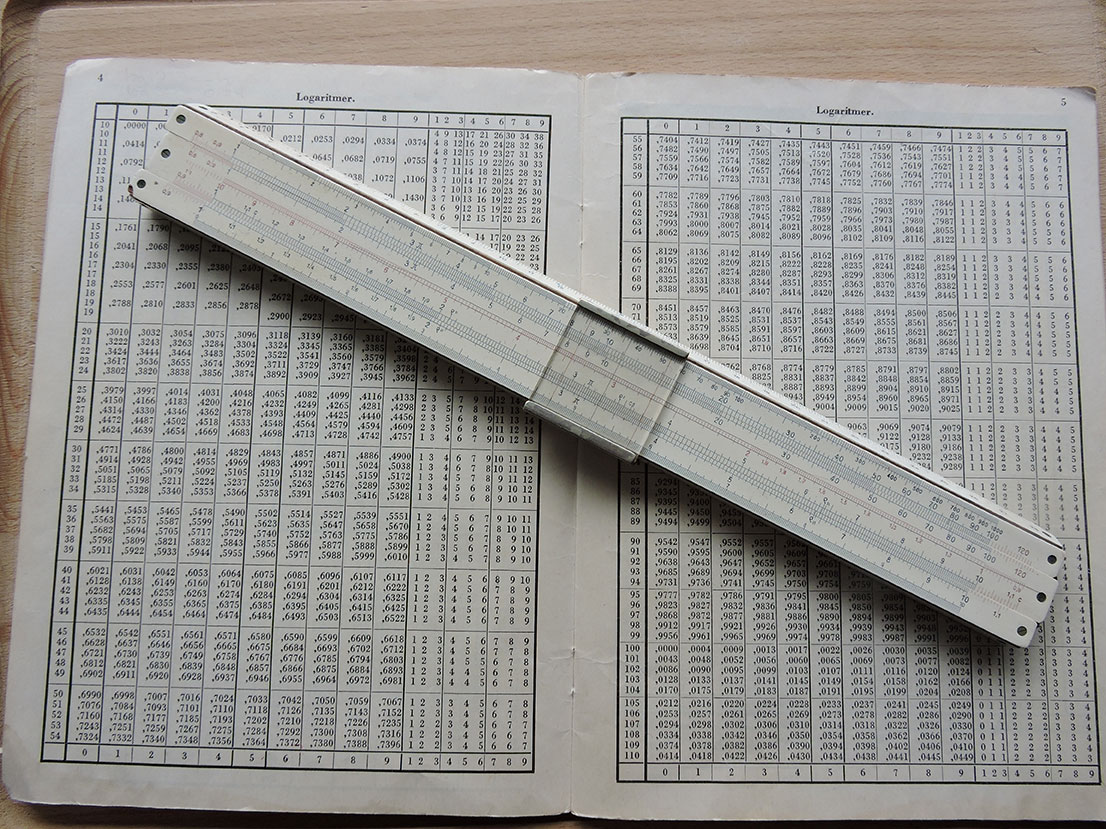
Undergnede brukte både regnestav og logaritmetabeller i 2.gym på reallinjen Grefsen hhøtere skole i 1966. Regnestaven er basert på logaritmiske akser. Dette var i tiden før lommekalkulatoren. Hvis man skulle multiplisere to store tall med hverandre kunne man istedet legge summere logaritmende til de to tallene. Det samme gjaldt dividering av to store tall, da kunne man subtrahere logaritmene til de to tallene dividend og divisor.
Mer historier om logaritmer
Det ble oppdaget lettere måter å trekke ut kvadratrøtter basert på bl.a. Isaac Newtonsoppdagelse av utvidelsen av uendelige rekker, Newtons generelle bionomialteorem:
\(\displaystyle\left(1+x \right)^k= 1 + kx + \frac{k(k-1)}{2\cdot 1}x^2+\frac{k(k-1)(k-2)}{3 \cdot 2\cdot 1}x^3+\frac{k(k-1)(k-2)(k-3)}{4 \cdot 3 \cdot 2\cdot 1}x^4+ \dots\)
Denne rekken gjelder også når x og k er uttrykt som en brøk
Den neste oppdagelsen er at Newton og Nicholas Mercator (1620-1687) uavhengig av hverandre fant at det er en sammenheng mellom logartimer og arealet under en hyperbel, og ved å bruke
\(\displaystyle\frac{1}{1+t}= (1+t) ^{-1}\)
og sette denne inn i Newtons generelle binomialteorem så kan integralet uttrykkes som en uendelig rekke:
\(\ln(1+x)= \displaystyle\int_ 0 ^x \frac{1}{1+t}dt= \int_0^x (1-t+ t^2-t^3+t^4 -\dots)dt= x-\frac{x^2}{2}+\frac{x^3}{3}- \frac{x^4}{4}+ \frac{x^5}{5}- \dots\)
Det betyr at man kan finne ln4= 3-32/2+33/3-34/4…
Det betyr også at man kan finne logartimer ved å beregne integralet under en hyperbel:

Vi kan nå f.eks. beregne logartimen til 1.5 som er lik arealet under hyperbelen fra 0-0.5:
\(\displaystyle\ln(1+0.5)=\ln(1.5)= \int_0^{0.5}\frac{1}{1+t}dt= 0.4054651\)
Logaritmer med basis eller grunntall e blir kalt naturlige logaritmer eller hyperbolske
Det neste store framskrittet skjer med Leonard Euler og publiseringen av tobindsverket Introductio in analysin infinitorum (1748). Euler hadde arbeidet med eksponenter av typen y=az hvor a>1. Han snudde problemet på hodet. Finn en verdi z slik at az=y, z blir derved en logaritme. Fra Euler kan vi skrive med moderne begrepsapparat.

\(\displaystyle z= \log_a(x)\;\; \text{hvis og bare hvis}\;\;\; a^z= x\)
Euler oppdaget også at hvis man kjenner loga(x) så er det lett å finne logaritmen med et annet grunntall logb(x)
\(z=\log _ b (x) \;\; \implies \; \; x= b^z\; \implies \log_a (x)= \log_a(b^z)= z \log_ab\)
Det vil si:
\(z=\log_b (x)= \displaystyle\frac{\log_a x}{\log_a b}\)
Dette gir den ”gyldne regel for logaritmer”: Forholdet mellom logaritmene til to tall blir det samme uansett hvilket grunntall (basis) man bruker:
\(\displaystyle\frac{\log_a x}{\log_a y}= \frac{\frac{log_a x}{\log_a b}}{\frac{log_a y}{\log_a b}}= \frac{\log_b x}{\log_b y}\)
Vi har som vist ovenfor:
\(\displaystyle \ln(1+x)= x- \frac{x^2}{2}+ \frac{x^3}{3}- \frac{x^4}{4}+ \dots \)
Ulempen er at denne rekken ikke når noen slutt. Euler valgte å erstatte x med –x:
\(\displaystyle \ln(1-x)= -x- \frac{x^2}{2}- \frac{x^3}{3}- \frac{x^4}{4}- \dots \)
Deretter trakk Euler disse to ligningene fra hverandre og fikk:
\(\displaystyle\ln\frac{1+x}{1-x}= 2\left(x+\frac{x^3}{3}+ \frac{x^5}{5}+ \frac{x^7}{7}+ \dots\right)\)
Nå var det en formel for logartimer som konvergerer som kan brukes til å finne logaritmer. Der hvor man tidligere var avhengig av en rekke kvadratrøtter var svaret nå en sum uten røtter.
Så utvidet Euler rekken ax ved hjelp av Newtons generelle binomialteorem og han endte opp med rekken:
\(\displaystyle a^x= 1+ kx + \frac{k^2}{2!}x^2+ \frac{k^3}{3!}x^3+\frac{k^4}{4!}x^4+\dots\)
Så satte han x=1=k og fikk:
\(a= \displaystyle 1+1+ \frac{1}{2!}+ \frac{1}{3!}+ \frac{1}{4!}+\dots\)
Og hvilket tall ble a ? Svar: 2.718281827459045235…
Det naturlige tallet e , innført av Euler, er summen av den uendelige rekken: hvor ! står for fakultet.