Alle naturlige tall, telletall, er enten et primtall eller produkt av primtall:
2,3,4 (2·2), 5, 6 (2·3 eller 3·2), 7, 8 (2·2·2), 9 (3·3), 10 (2·5), 11, 12 (2·2·2),13, 14 (2·7), 15,....
En unike mengden i produktet kalles primfaktorer eller primtallsfaktorer. Bare det første primtallet 2 er et partall, resten av primtallene er oddetall.
Alle de naturlige tallene 1, 2, 3, osv. kan lages ved 1+1+1+1 osv. og neste talle er 1 større enn det foregående. Hvis vi har tallet 12 vet vi at 12 = 4·3 og 3 og 4 kalles faktorer av 12. Vi har generelt for et tall m at m = n∙k , hvor tallene n og k (kvotient) er faktorene til m. Går ikke divisjonen opp blir det en rest som er mindre eller lik tallet vi deler på. For eksempel 16:5= 3 og en rest r=1.
Fundamentalteoremet i aritmetikk (tallregning) sier at ethvert positivt heltall n kan uttrykkes som et produkt av en unik samling av primtall p1, p2, p3,… hvor a, b, c,… angir hvor mange ganger primtallet forekommer.
\(n=p_1^a \cdot p_2^b \cdot p_3^c \cdot \dots\)
Delingsalgoritmen: Hvis m og n er naturlige tall så finnes det en unik k og r slik at:
\(m=n \cdot k + r \;\;\; hvor\; \; \; 0\leq r\leq n-1\)
De 200 første primtallene:
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 133 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 259 263 269 271 277 281 283 293 301 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 511 521 523 541 547 553 557 559 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 793 797 809 811 817 821 823 827 829 839 853 857 859 863 871 877 881 883 887 889 907 911 919 929 937 941 947 953 967 971 977 983 991 997 1009 1013 1019 1021 1031 1033 1039 1049 1051 1061 1063 1069 1087 1091 1093 1097 1103 1109 1117 1123 1129
Gauss og Legendre fant at andelen av primtall blant de naturlige tallene fulgte forholdet 1/ln(n). Jo større primtallene blir, desto sjeldnere forekommer de.
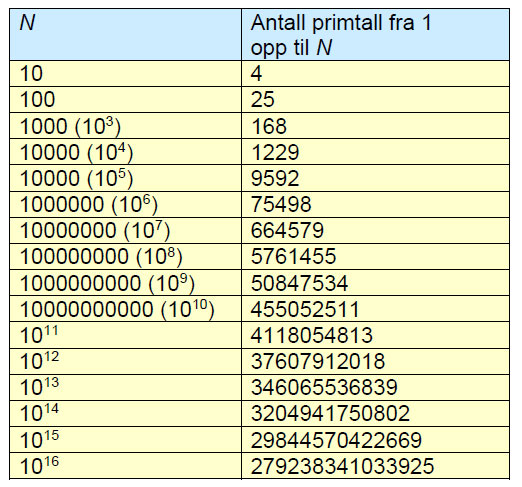
Blant de første tallene forekommer primtallene oftere enn lenger ut i tallrekken. Hvor mange primtall finnes det ? Hvordan er fordelingen av primtall utover i tallrekken ? Den minste avstanden mellom to primtall er mellom 2 og 3. Ender et tall på 0, 2, 4, 6, eller 8 er det ikke et primtall. Primtallene på ende på 1, 3, 7, eller 9, siden tall som ender på 5 er delelig med 5.
Euklid brukte kontradiksjonsprinsippet og viste at det var uendelig mange primtall.
Gauss formodning (konjektur)
Gauss konjektur (formodning) gir en gjetning om antall primtall i form av et logaritmisk integral, og gjetningen blir mer og mer riktig ettersom N øker. Carl Gauss og den franske astronomen og matematikeren Adrien Marie Legendre (1752-1833) fant at andelen av primtall blant de naturlige tallene fulgte tilnærmet forholdet n/ln(n). Primtallsteoremet ble bevist i 1896 av Jacques Hadamard og Charles-Jean de la Vallée Poussin.
Primtallesteoremet (Carl Gauss 1792): Når n går mot uendelig blir antall primtall ≤ n lik:
\(\approx\displaystyle\frac{n}{\ln n}\)
Antall primtall N er ca. lik arealet under kurven y=1/ln(x) mellom x=2 og x=N, det logaritmiske integralet til N, også oppdaget av Gauss.
\(\displaystyle\int_ 2^n \frac{1}{\ln x}dx\)
Tvillingprimtall
Tvillingprimtall (primtallstvillinger) er primtall med to påhverandre følgende primtall av oddetalltypen 3 og 5; 5 og 7; 11 og 13 osv. Finnes det uendelig mange slike par ? Den norske matematikeren Viggo Brun (1885-1978) arbeidet med denne problemstillingen. Antall primtallspar er proporsjonal med x/(lnx)2 og for store x er antall primtallspar <100x/(lnx)2. Hvis man tar den resiproke av primtalltvillinger og summerer dem får man en rekke som konvergerer mot Bruns sum 1.90216….
\(\left(\frac{1}{3}+\frac{1}{5}\right)+\left(\frac{1}{5}+\frac{1}{7}\right)+\left(\frac{1}{11}+\frac{1}{13}\right)+\left(\frac{1}{17}+\frac{1}{19}\right)+\left(\frac{1}{41}+\frac{1}{43}\right)+\left(\frac{1}{59}+\frac{1}{61}\right)+\dots\)
De neste primtallsparene er 71-73, 101-103, 107-109, 137-139, 149-151, 179-181, 191-193 og 197-199. For x opp til 103 finnes 35 primtallspar, opp til 104 finnes 205 og opp til 105 finnes 1224 osv.Hvis p er et odde primtall kan det uttrykkes som sum av to kvadrattal hvis og bare hvis p er kongruent modulo 4 med rest 1 (modulær aritmetikk)
\(p \equiv 1(\mod 4)\)
e.g. 17 dividert på fire gir rest 1
\(17 \equiv 1 (\mod4)\)
For eksempel 5=12+ 22; 13= 22+ 32; 17= 12 + 42 ; 29=22 + 52
Primtallet p er et Gaussheltall hvis det finnes to heltall a og b slik at:
\(p= a^2 + b^2=(a+bi)(a-bi)\)
hvor i er den imaginære enhet i2=-1.
Gauss kunne vise den kvadratiske resiprositetsloven:
\(x^2\bmod p=q\)
hvor både p og q er primtall.
31, 331, 3331, 33331 osv. er primtall, men når man kommer til 333333331 så er ikke dette et primtall: 17·19607843 = 333333331
Mersenneprimtall
Den franske presten Marin Mersenne (1588-1648) viste viste i Cogitata Physica-Mathematica (1644) at 2n-1 er primtall kalt Mersenne primtall, men gjelder ikke alle (kjenner til 32 unntak).
23-1= 7 , 25-1= 31, 27-1 = 127, 213-1 = 8191 Man vet ikke om det finnes et uendelig antall Mersenneprimtall.

Frimerke som viser et av Mersenneprimtallene
Man kjernner til 47 Mersenneprimtall hvor det største Her 43 Mersenneprimtall 43. oppdaget i 2005 og har 9152052 siffer
2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503, 132049, 216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377, 6972593, 13466917, 20996011, 24036583, 25964951, 30402457
Goldbachs formodning
Goldbachs formodning (Christian Goldbach 1690-1764), i et brev til Euler i 1742, skrev at ethvert liketall større enn 2 kan skrives som summen av to primtall: 4=2+2; 6=3+3. For noen er det flere muligheter: 24=5+19=7+17=11+13.
Alle hele tall >5 kan skrives som summen av tre primtall.
Følgende formel gjelder for mange tilfeller, men ikke alle:
Hvis p1, p2 osv. er primtall så vil p1∙p2∙p3∙∙∙pn + 1 være et primtall: (2∙3∙5)+1= 31
Ethvert positivt tall >1 kan skrives som et produkt av to eller flere primtall. Den ungarske matematikeren Paul Erdös (1913-1996) viste at det kan alltid finnes et primtall mellom ethvert heltall n og 2n, for eksempel mellom 2 og 4, 8 og 16 osv.
Primtall i 4n+1 familien er: 5,13,17,29,37,41,53,61,73,89,97
Primtall i 4n-1 familien er: 3,7,11,19,23,31,43,47,59,67,71,79,83
Alle tall av typen:
\({2^2}^n\)
er primtall (Fermats konjektur(formodning)).
Fermats lille sats (1640):
Hvis p er et primtall og a er et heltall så er ap-a delelig med p.
Stanislaw M. Ulam (1909-1984) fant et spiralmønster i primtallene, Ulam spiral, vist i populærutgave av Martin Gardners Matheamtical games i tidsskriftet Scientific American Hvis alle heltallene skrives som enspiral i et kvadrat så vil de fleste primtallene samle seg ved diagonallinjene. Ulam spiral er også tilknyttet Landaus problemer om primtall presentert av den tyske matematikeren Edmund Landau 1877-1938). på en internasjonalmatematikerkonferanse i 1912. Landaus problemer omfatter Goldbachs konjektur, primtallskonjekturen, Legendres konjetur og spørsmålet om det finnes et uendelig tanall primtall av typen p = n2+ 1 (nær kvadratprimtall)? Fermats primtall er et eksempel på nær kvadratprimtall
Astronomen, matematikeren og lederen av biblioteket i Alexandria Eratosthenes (276-195 f.kr.), også kjent for beregning av omkretsen av Jorden, laget Eratosthenes sil som sier hvis n er et sammensatt tall så vil minst en av primfaktorene til n være mindre eller lik kvadratroten til n. Denne silen er best egnet hvis det bare er to primfaktorer.
Matematikeren Edward Waring utviklet et teorem for å finne hva som er primtall, kalt Wilsons teorem (oppkalt etter hans venn matematikeren John Wilson (1741-1793):
p et primtall hvis og bare hvis (p-1)!+1 er delelig på p.
(p-1)! vil så å multiplisere alle tallene fra 1 til p-1
Eksempel p=7 gir (7-1)!= 6! = 6∙5∙4∙3∙2∙1 = 720. Legg til 1 og vi ser at tallet er delelig på 7, altså er 7 et primtall. Wilsons teorem er grei for små tall, men n fakultet (n!), fakultetsfunksjonen, har en ulempte at den blir gedigen når n øker.
Den franske matematikeren Joseph Bertrand (1822-1900) kunne i Cacul de probabilités (1845) finne en konjektur (Bertrands konjektur eller formodning):
For n≥ 2 så finnes det minst ett primtall mellom n og 2n.
Dette ble seinere bevist av den russiske matematikeren Pafnuti Lvovich Tchebychef (1821-1894).
For neste primtall pn+1 så vil dette alltid bli mindre enn 2 ganger det forrige primtallet pn:
\(p_{n+1}<2p_n\)
Vi har også at summerer du to påfølgende primtall pn+1 og pn så vil summen av dem pn+2 være større enn det neste primtallet:
\(p_n + p_{n+1}>p_{n+2}\)
Produktet at to primtall pm∙pn vil alltid være større enn summen av dem:
\(p_m \cdot p_n>p_{m+n}\)
Euler oppdaget at funksjonen:
\(f(x)= x^2 + x + 41\)
genererer primtall for x=[0,39].
41 43 47 53 61 71 83 97 113 131 151 173 197 223 251
281 313 347 383 421 461 503 547 593 641 691 743 797 853 911 971 1033 1097 1163 1231 1301 1373 1447 1523 1601
Andre funksjoner som gir mange primtall er
f(x)=2x2-199; f(x)=6x+5
f(x)=30x – 13.
Det er lett etter mange tester for å finne ut om et tall er et primtall eller ikke. Ender tallet >2 på 0,2,4,6 eller 8 er det ikke et primtall.
Med avanserte datamaskiner letes det etter de største primtallene. Faktorisering av store primtall danner basis for noen av metodene anvendt innen kryptografi.
Det finnes uendelig mange primtall.
Ifølge Eulers formel er:
\(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n}=\prod \frac{1}{1-\frac{1}{p}}\)
hvor p er primtall.
Ethvert positivt tall kan uttrykkes som et unikt produkt av primtall.
Leopold Kronecker (1823-1891) kunne videreutvikle denne for s > 1:
\(\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^s}=\prod \frac{1}{1-\frac{1}{p^s}}\)
Heltallsverdiene s kan uttrykkes som zeta s (ζ(s)) i Eulers zetafunksjon hvor det er en sammenheng rekken av alle de positive tallene og produktet av alle primtallene !
\(\zeta(s)=\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^s}=\frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\dots =\left(\frac{1}{1-2^s}\right)\left(\frac{1}{1-3^s}\right)\left(\frac{1}{1-5^s}\right) \dots \)
For s≤ 1 gir dette en uendelig sum som har et uendelig svar, men for s>1 har summen en endelig verdi.
Euler fant at for den konvergente uendelig rekken ζ(2) = π2/6 og nok en gang dukker pi opp på et underlig sted.
\(\zeta(2)=\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^2}=1+\frac{1}{4} +\frac{1}{9}+\frac{1}{16}+\frac{1}{25} \dots=\frac{\pi^2}{6}\)
for ζ(4)=π4/90 blir det en konvergent uendelig rekke:
\(\zeta(4)=\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^4}=1+\frac{1}{16} +\frac{1}{81}+\frac{1}{256}+\frac{1}{625} \dots=\frac{\pi^4}{90}\)
ζ(3)=1.202… (Apérys konstant.
Verdien av zetafunksjonen for reelle tall for s fra 0 til 4

Riemanns zetafunksjon
Riemanns zetafunksjon har sitt utgangspunkt i Eulers formel (Eulers zetafunksjon), og uttrykker summen av inverse potenser av positive tall. Riemann utvider den til å omfatte de komplekse tallene. Riemanns zetafunksjon treffer man på i de underligste sammenhenger innen naturvitenskap.

Bernhard Riemann studerte forskjellen mellom reelle og komplekse funksjoner. Hvis vi har to komplekse tall z=x+iy og w=u+iv så vil grensen for dw/dz være den deriverte akkurat som for de reelle tallene.
Heltallsverdiene s kan uttrykkes som zeta s (ζ(s)):
\(\zeta(s)=\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^s}=1+\frac{1}{1^s} +\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s} \dots\)
Vi definerer Riemanns zeta-funksjon som:
\(\zeta(s)=\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^s}\)
Laurent-rekke utvidelse av zeta-funksjonen er:
\(\zeta(s)=\frac{1}{s-1}+\displaystyle\sum_{n=0}^{\infty}\frac{{-1}^n}{n!}\gamma_n{(s-1)}^n\)
hvor Stieltjes konstant γn (gamma n)er lik:
\(\gamma_n=\displaystyle\lim_{m \to \infty}\left(\left(\sum_{k=1}^{m}\frac{(\ln k)^n}{k}\right)-\frac{(\ln m)^{n+1}}{n+1}\right)\)
En Laurent-rekke er en potensrekke for en kompleks funksjon f(z) og som inneholder med negative ledd.
Vi kan finne verdien for Stieltjes konstant ved forskjellige verdier av n. Hvis n=0 blir Stieltjes konstant lik Euler-Mascheroni-konstanten (gammakonstanten).
Det viser seg at Riemanns zetafunksjon er koblet til fordelingen av primtall (Über de Anzahl der Primzahlen unter einer gegebener Grösse (1859)). Primtallsteoremet kan utledes fra nullene i zetafunksjon hvor nullene i kompleksplanet ligger symmetrisk på en linje.
Riemann uttrykte ζ(s) i form av integraler, og viste at det gjaldt for hele kompleksplanet. Ifølge Riemann har alle komplekse null av ζ(s) en reell del lik ½.
Hvis s er et komplekst tall s=a+bi
så vil alle løsninger av ligningen nedenfor bli et komplekst tall hvor a=1/2
\(\displaystyle 1-\frac{1}{2^s}+\frac{1}{3^s}-\frac{1}{4^s}+ \frac{1}{5^s}\dots=0\)
Det vil si at alle løsningene blir liggende på en rett linje i kompleksplanet med a=1/2, avgrenset av [0,1] på den reelle aksen, og altså parallell med den imaginære aksen. Noen av de første ikke-trivielle løsningene er de komplekse 0.5+14.135i; 0.5+21.022i; 0.5+25.011; og 0.5+30.425i
Hva nå hvis vi setter s=-1 ?
\(\zeta(-1)=\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^{-1}}=1+\frac{1}{1^{-1}} +\frac{1}{2^{-1}}+\frac{1}{3^{-1}}+\frac{1}{4^{-1}} \dots=1 + 2+ 3+ 4+\dots=\infty\)
Vi får da en divergent rekke hvor summen blir stadig større etter hvert som n øker.
Riemann utvidet funksjonen til:
\(\zeta(s)=\displaystyle\frac{\prod(-s)}{2\pi i}\int_C\frac{(-x)^s}{e^x-1}\frac{dx}{x}\)
Den funksjonelle ligning av Riemanns zetafunksjon gjør det mulig å regne ut zetafunksjonen for s=-1:
\(\zeta(s)=2^s\pi^{s-1}\sin \left(\frac{\pi s}{2}\right)\Gamma (1-s)\zeta(1-s)\)
\(\Gamma\) er gamma
Hvis vi regner ut for ζ(-1):
\(\displaystyle \zeta(-1)=2^{-1}\pi^{-2}\sin \left(\frac{-\pi }{2}\right)\Gamma (2)\zeta(2)\)
hvor \(\zeta(2)=\frac{\pi ^2}{6}\)
Vi har nå vist at:
\(1 + 2+ 3 +4 + 5 \dots=-\frac{1}{12}\)
Et helt ulogisk regnestykke, hva er det som skjer ? Biologen har ramlet av lasset for lenge siden.
Vi kan se at zeta-funksjonen blir lik 0 for flere negative verdier, for negative liketall:ζ(-2)=0, ζ(-4)=0,ζ(-6)=0 osv.
Disse kalles trivielle null.
Riemannfunksjonen R(n) gir et mye bedre estimat av antall primtall i tallrekken, enn det Euler, Legendre og Gauss hadde klart, som viste at et estimat antall primtall fulgte funksjonen:
\(\displaystyle \text{antall primtall}\approx\frac{n}{\ln n}\)
og fra Riemannfunksjonen et bedre estimat:
\(\displaystyle \text{antall primtall}=R(n)-\displaystyle\sum_{\rho}^{\infty}R(n^\rho)\)
hvor rho (ρ) er ikke trivielle 0 på linjen 0.5+xi.
Andricias konjektur eller formodning (Dorin Andricia) tar for seg avstanden mellom primtall, og viser at denne differansen er mindre enn 1:
\(\displaystyle A=\sqrt{p_{n+1}}-\sqrt{p_ n}<1\)
hvor pn er det n-te primtall. Den høyeste verdien for A er ved n = 4, og lik 0.67087…
Den minste avstanden for de 100000 første primtallene er 0.0009579968 og dette skjer for primtall nr. 99998
Goldbachs binære konjektur (Christian Goldbach 1690-1764): ethvert liketall større enn 4 (>4) kan uttrykkes som en sum av to primtall: 4 = 2+2; 6 = 3 +3; 8=3+5, 10=3+7 og 5+5, 12=5+7, 14=3+11 og 7+7…
For noen av partallene er det flere måter å uttrykke summen. For 34 er det fire måter: 17+17, 11+23, 3+31, 5+29. Dette tallet, C(34)=4, kalles Goldbachs tall.
Goldbachs ternære konjektur: Ethvert oddetall >7 kan uttrykkes som en sum av tre primtall.
Möbiusfunksjonen
August Ferdinand Möbius (1790-1868), kjent for Möbiusbåndet i topologi, student hos Gauss, utviklet en Möbiusfunksjon M(n):
M(n)=0 hvis et av primtallene i faktoriseringen av n har eksponenten 2 eller mer.
M(n)=1 hvis antall forskjellige primtall i faktoriseringen av n er et liketall
M(n)=-1 hvis antall forskjellige primtall i faktoriseringen av n er et oddetall.
M(0)=1;M(1)=1,M(2)=-1;M(4)=0;M(5)=-1;M(6)=1;M(7)=-1;M(8)=0;M(9)=0;M(10)=1
Det viser seg at Möbiusfunksjonen er relatert til den inverse av zetafunksjonen.
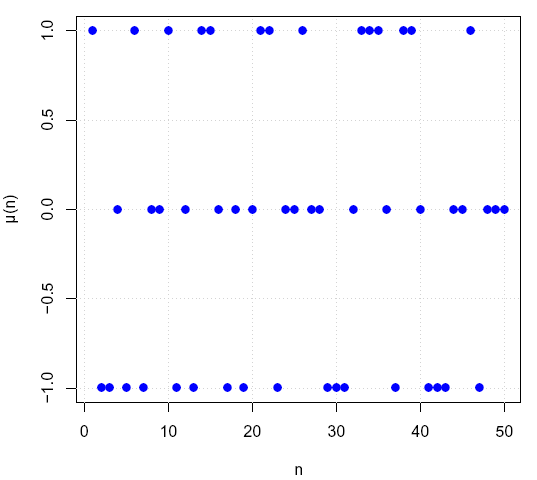
Möbiusfunksjonen.