I dette eksemplet ser vi på sannsynligheten for å trekke første hjerter fra en godt stokket kortstokk. Legg merke til forskjellen mellom antall kort før første hjerter og antall kort til og med første hjerter. I vårt tilfelle brukt antall kort til og med første hjerter. Man kan også velge første spar, kløver eller ruter hvis man foretrekker det.

Hvert kort fra kortstokken har samme sannsynlighet for å bli trukket. I en kortstokk er det 52 mulige utfall og utfallsrommet er:
S = {13 kløver (♣), 13 ruter (♦), 13 hjerter (♥), 13 spar (♠)}
Sannsynlighetene for de enkelte elementene i utfallsrommet S til en kortstokk 1/52.
Sannsynligheten for å trekke ut en hjerter fra kortstokken 13/52.
13 hjerter kan stokkes inn på:
\(\displaystyle{52 \choose 13}\)
forskjellige måter. Første hjerter ligger som nummer k, de resterende hjerter ligger som
\(\displaystyle {52-k \choose 12}\)
Sannsynligheten for gunstig utfall X = k blir:
\(\displaystyle P\left(X = k \right)=\frac{52-k \choose12}{52\choose 12}\)
Minner om fakultetsfunksjonen n! hvor:
\(\displaystyle \frac{n!}{k! (n-k)!}= {n \choose k}\)
Geometrisk og negativ binomial sannsynlighetsfordeling
Både geometrisk sannsynlighetsfordeling og negativ binomial sannsynlighetsfordeling kan brukes til å beskrive antall forsøk for å få et bestemt utfall. Dette er diskrete (diskontinuerlige) sannsynlighetsfordelinger. Vi gjentar en rekke uavhengige Bernoulli-forsøk (to mulige utkomme: suksess eller ikke-suksess) før suksess skjer. Vi lar variabelen X være antall forsøk som trengs for å få utkomme suksess. Vær oppmerksom på at det finnes to utgaver av geometrisk fordeling.
Hvis sannsynligheten for suksess i et forsøk er lik p, ikke-suksess q = 1-p, så vil sannsynligheten for at variabel X får en spesiell verdi bli:
\(\displaystyle P \left(X=n\right)=pq^{n-1}\)
som er den geometriske fordelingen, hvor n er antall forsøk før suksess. P(X = n) er sannsynligheten for første suksess kommer i forsøk nummer n.
Sannsynligheten for flere enn n forsøk før suksess blir:
\(\displaystyle P\left(X>n\right)=q^n\)
Sannsynligheten for n eller mindre forsøk før suksess blir:
\(P\left(X\leq 1\right)=1-q^n\)
Forventning E(X) for en geometrisk sannsynlighetsfordeling:
\(E\left(X\right)=\frac{1}{p}\)
Varians (Var (X)) er:
\(Var\left(X\right)=E\left(X^2\right)-E^2\left(X\right)=\frac{q}{p^2}\)
Negativ binomialfordeling beskriver antall forsøk opp til et bestemt antall suksesser, mens den geometriske fordeling er et spesialtilfelle som beskriver antall forsøk opp til første suksess.
I vårt eksperiment teller vi antall kort med variabel X = k hvor k er antall kort til og med første hjerter. Resultat fra kurset BIO2150 Biostatistikk og studiedesign (nedlagt 2018), IBV, UiO.
Vi forutsetter at kortstokken er godt stokket før du begynner.
Noter hvor mange kort du må trekke til og med første hjerter. Gjør dette 20 ganger. Før resultat i fellesskjema ved tavle. Fellesresultat kull 2014-2017:
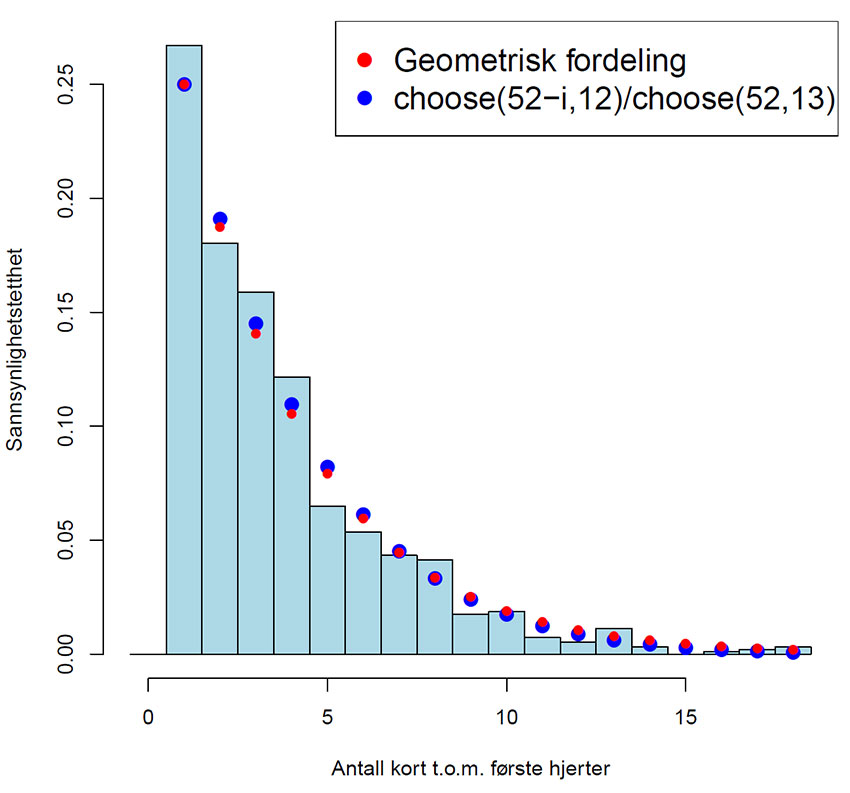
Figur viser fellesresultat, samt både resultat fra geometrisk sannsynlighetsfordeling, og binomialformelen vist over. Leser man nøye i ?dgeom så bruker R antall feil før suksess , mens vi har i vårt tilfelle brukt antall kort til og med første hjerter. På figuren er det korrigert for dette. Kortstokkdatasett
På hvor mange måter kan 13 hjerter plasseres i en kortstokk ?13 hjerter kan plasseres i stokken på 635013559600 forskjellige måter, når rekkefølgen ikke teller:
\({52 \choose 13}= 635013559600\)
I kortspillet poker deles det vanligvis ut fem kort. Hvor mange forskjellige 5 kort-kombinasjoner er det mulig å dele ut fra en vanlig kortstokk med 52 kort?
\({52 \choose 5}= 2598960\)
Det er 52 fakultet (52!) mulige måter å stokke en kortstokk, et gigantisk tall, mer enn 80 undersillioner.
ca. 8·1067, et tall med 67 siffer
R Core Team (2016). R: A language and environment for statistical
computing. R Foundation for Statistical Computing, Vienna, Austria.
URL https://www.R-project.org/.