Man finner speilbilder og minst ett symmetriplan. Symmetri representerer balanse, orden og regelmessighet, og er koblet til skjønnhet og harmoni slik mennesket oppfatter det. Asymmetri og ubalanse blir selektert vekk i biologiske reproduktive systemer med aktivt partnervalg (seksuell seleksjon). Mennesket er ca. venstre/høyre symmetrisk. Når man går brytes symmetrien, hvor det ene beinet og armen er tidsforskjøvet i forhold til den andre.
Gruppeteori
En av grunnleggerne av gruppeteorien i matematikk var franskmannen Évariste Galois (1811-1832), som viste at alle ligninger kan tilordnes en gruppe.

Galois led en tragisk skjebne. Liten interesse for bl.a. latin og retorikk gjorde at Galois strøk på opptaksprøven til den prestisjefylte École Polytechnique, grunnlagt av Lagrange. Galois utførte beregninger og resonnementer i hodet, og det passet dårlig for eksaminatorer som ville ha detaljer, og det endte med at han strøk i siste opptaksprøve i matematikk, hvor han kastet en svamp i hodet på en av eksaminatorene. Galois begynte på École normale, men ble relegert pga. revolusjonær obsternasighet, ble satt i fengel, forsøkte å tjene penger som matematikklærer, og døde etter i en duell. Galois leste lærebøkene til Legendre, Théorie des nombres (Teoriene om tallene) Élémentes de la géométrie (1794). Legendre arbeidet ved Bureau des longitudes og utførte lengdegradmålinger sammen med Cassini og Méchain. I 1795 ble meridianbuen Barcelona-Dunkirk målt, og dannet grunnlaget for meter. Legendre er også kjent for sine studier av eliptiske integraler og funksjoner, Traité des functions elliptique (1827), samt den kvadratiske resiprositetsloven. Manuskriptene til Galois var det få som forstod.

Joseph Louis Lagrange (1736-1813) var den første matematikkprofessor ved École Polytechnique, og etterfulgte Euler som president i Berlin-akademiet.

Napoleon og Frankrike var tidlig ute med å innføre metersystemet, og Lagrange var leder av meterkomitéen. Kanskje grunnen til at britene holder på sitt gamle målesystem, var skepsis til det som kom fra Frankrike ? Galois-teori omhandler løsning av algebraiske ligninger ved hjelp av rottegn. Galois fant at femtegradsligninger kan ikke løses med formler på grunn av feil symmetri. Symmetrier har nær tilknytning til grupper. Grafiske mønstre finner vi i tepper, tapeter, mosaikker, og krystaller, og det er et maksimalt antall hovedmønstre, i alt 17. Også for disse finnes det transformasjoner som bevarer mønsteret uforanderlig.
Niels Henrik Abel (1802-1929) og og Marius Sophus Lie (1842-1899) er norske matematikere som har fått sine navn knyttet til grupper.



Sophus Lie
Lie-grupper har i dag fått fornyet interesse med E8-matematikk og studiet av differensialligninger og manifold-topologi.
Sophus Lie (1842-1899), som sammen med N.H. Abel er en av Norges mest kjente matematikere, utviklet teorien om tranformasjonsgrupper (Lie-grupper). E8-matematikk i et 8-dimensjonalt rom er relatert til Lie-grupper og Lie-algebra med 248 dimensjoner. Det finnes en Lie-algebra En for alle heltall n≥3, men får dimensjonen uendelig når n>8. Røttene i E8 er et rang 8 rotsystem med 240 røtter i R8, og rotvektorene har samme lengde, noen ganger satt lik kvadratroten til 2 (√2). Det fascinerende er at E8 Lie-algebra med tilhørende symmetrier gjenfinnes i den virkelige verden som basis for strengteori, ”teorien om alt” og supergravitasjon i teoretisk fysikk, samt i elektronspin i atomer (kobolt-niobkrystaller kjølt ned mot det absolutte nullpunkt). ”Teorien om alt” forsøker å forene gravitasjon og kvantemekanikk. Da matematikere hadde løst E8 ble dette annonsert i den amerikanske kongressen (se YouTube).

E8 er en 248-dimensjonal Lie-gruppe
Gruppeteori baserer seg på tallteori, studiet av algebraiske ligninger og geometri.
Abel led en tragisk skjebne, men på en annen måte enn Galois. På Katedralskolen i Christiania kom Abel i kontakt med matematikklærer Bernt Michael Holmboe (1795-1850), som utga flere lærebøker i matematikk og som seinere ble professor ved Universitetet i Christiania. I 1821 ble Abel student ved universitetet. Paolo Ruffini hadde i 1799 vist at femtegradsligninger tilsynelatende ikke hadde generelle løsninger ved rotuttrykk, men det manglet det fullstendige bevis, Cauchy mente at dette var av mindre betydning, men det var Niels Henrik Abel som i 1824 kom med det endelige beviset for at femtegradsligninger kan ikke løses ved rottegn, Abel-Ruffini-teoremet. Med statsstipend reiste Abel til Berlin i 1825 hvor han møtte August Leopold Crelle (1780-1855), grunnlegger av Journal für die reine und angewandte Matematik, Crelles journal, hvor mange av Abels arbeider ble publisert. Oppholdet i Paris i 1926 ble ikke som Abel hadde håpet og ventet. I Frankrike arbeidet både Augustin-Louis Cauchy (1789-1857) og Legendre, som Abel hadde ønsket å møte.

Cauchy er kjent for definisjonen av hva kontinuerlig betyr, noe som er intuitivt lett å forstå hva er, men er vanskelig å definere. Han definerte også grensebegrepet. Cauchys middelverdiformel omhandler to funksjoner definert over samme intervall, og Cours d’analyse algébrique (1821) dannet grunnlag for teoriene om konvergens og divergens.
Abels Mémoire sur une propritété générale d’une classe trés étendue des fontions trenscendantes (Paris-avhandlingen), som Abel selv hadde store forhåpninger til, ble liggende nedstøvet og glemt på Cauchys skrivebord, og ble først publisert i 1841. Abel arbeidet også med eliptiske funksjoner, et tema som også den tyske matematikeren Carl Gustav Jacob Jacobi (1804-1851) arbeidet med. Jacobi hadde i sine ungdomsår interessert seg for løsning av femtegradsligninger. Jacobi har gitt navn til Jacobi-determinanter med de partiellderiverte av funksjoner. Er Jacobi-determinanten lik null er funksjonene avhengig av hverandre. Jfr. også Jacobi-matriser.
Abel fikk ikke jobb ved Universitetet i Christiania, bortsett fra ettårs vikariat for Christopher Hansteen i 1827, da Abel kom tilbake til Norge uten noen jobb å gi til. Finansdepartmentet hadde sagt nei til å forlenge Abels stipend. Skuffelsen var stor hos mange da Holmboe i 1825 overtok Søren Rasmussens (1768-1850) professorat i fysikk og matematikk ved Universitetet i Christiania, og ikke Abel, visstnok pga. av Abels manglende pedagogisk kompetanse. Franske matematikere hadde også øvet påtrykk på kong Karl Johan for å skaffe Abel en stilling ved universitetet. Som så mange på den tiden ble Abel rammet av fattigmannssykdommen tuberkulose, og han døde i 1829, 26 år gammel, to dager før Crelle, Abels utrettelige forkjemper, kunne meddele at Abel var blitt kallet til et professorat ved Universitet i Berlin. Holmboe fikk utgitt Abels arbeider i tobindsverket Oeuvres complétes de N.H. Abel i 1839, ti år etter Abels død.
Ved Abelhaugen, Slottsparken i Oslo, står Vigelands berømte bronsestatue av Niels Henrik Abel, monumentet avduket i 1908. Den er verdt et besøk, og minner oss om hvordan Norge tok vare på et av sine største genier.
Det finnes en rekke grupper: Abelske-, Lie-,permutasjons-, matriks-(lineære-), algebraiske-, topologiske-, abstrakte-, geometriske- og kombinatoriske-. Et annet eksempel på grupper er Fischer-Griess Monster M(Bernd Fischer og Robert Griess):
\(2^{46}\cdot 3^{20} \cdot 5^9 \cdot 7^6 \cdot 11^2 \cdot13^3 \cdot 17\cdot19\cdot23\cdot29\cdot31\cdot41\cdot47\cdot59\cdot 71\)
Monster inngår som en del av Conway og Norton´s måneskinnskonjektur og det finnes tilknytninger til Dynkin-diagram E8.
Den sykliske gruppen Z/26 bestående av bokstavene i det engelske alfabetet danner grunnlaget for Caesar-koding, en av de første metodene brukt innen kryptografi.

Det er en sammenheng mellom symmetri og topologi. Topologi kalles også gummigeometri hvor den geometriske formen på figurer beholdes når den dreies, strekkes, vris eller presses sammen. Det må imidlertid ikke lages kutt i gummien.
To symmetrier gir en tredje symmetri. Et kvadrat, gruppen D4 har 8 symmetrier, 4 rotasjoner og 4 speilinger om aksene (horisontal-, vertikal akse og to diagonaler). Viser man noe i ett hjørne, så vet man hva som vil skje i de andre hjørnene ut fra symmetri. Hvis vi har et kvadrat festet til et punkt i midten så kan dette roteres 90o tre ganger med klokka rotasjon r1, r2 og r3 og så den siste rotasjonen r0 som gir det opprinnelige kvadratet. Man kan også betrakte denne siste rotasjonen som om man roterte det opprinnelige kvadratet 0o og så er man tilbake til utgangspunktet.
Vi betegner de fire rotasjonene R4={r0, r1, r2, r3}, som er en Abelsk undergruppe av D4, selv om D4 i seg selv er ikke-Abelsk.

Mengden av hjørnene S={A,B,C,D} har 4!=24 muligheter for sortering, men alle disse er ikke mulige slik at vi allikevel ender bare opp med 8 symmetrier.
Vi kan også betrakte rotasjonene som at det skjer transformasjoner av kvadratet inn i seg selv hvor alle avstander beholdes i sin opprinnelige form. Dette fører fram til begrepet transformasjonsgrupper.
Vi kan også lage speilinger omkring 4 akser, x- og y-aksen og to diagonale akser.
Vi betegner de 4 speilingene S4={s1, s2, s3, s4}, hvor s1 er speiling om x-aksen, s2 omkring y-aksen, s3 omkring diagonalen BD og s4 omkring diagonalen AC
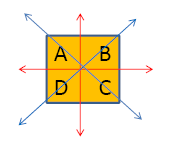
Vi ser at hvis vi e.g. holder BD fast og vipper rundt diagonalen så vil A og C bytte plass, men vi legger merke til at det er mulig å få samme resultat ved en rotasjon.

Speiler vi ennå en gang om den samme aksen ved å holde BD fast kommer vi tilbake til utgangspunktet:
Hvis vi betegner e for et identitetselement, den opprinnelige utgangsfirkanten i vårt tilfelle, ser vi at 2 speilinger S og S gir identitetselementet e:
\(S\cdot S=e\)
og 4 rotasjoner R4 bringer oss også tilbake til utgangsfirkanten:
\(R^4=e\)
Identitetselementet tilsvarer tallet 1 i vanlig multiplikasjon. Legg merke til at vi bruker multiplikasjonstegn selv om dette er en mer abstrakt form for multiplikasjon.
Hvis vi betrakter en rotasjon med klokka for R så er det også en rotasjon mot klokka R-1, og hvis vi først roterer en gang 90o med klokka og en gang 90o mot klokka, så er man tilbake til utgangspunktet. Elementet har en invers, en inverstransformasjon. Hvert element i en gruppe må ha en invers.
\(R\cdot R^{-1}=e\)
Vi ser også at en speiling S og en rotasjon 90o med klokka R er lik en rotasjon 90o mot klokka etterfulgt av en speiling:
\(S\cdot R=R^{-1}\cdot S\)
Legg merke til at vi nå er iferd med å utvikle et sett regneregler for kvadratet vårt, kalt D4 (dihedral gruppe). Hvis S er en speiling så finnes det også en invers speiltransformasjon S-1 i gruppen. Dessuten, hvis R er en rotasjon og S er en speiling så finnes det også et produkt R∙S. Det er ikke nødvendigvis slik at R∙S=S∙R, men hvis de er det kalles gruppen Abelsk (kommutativ).
Generelt er en gruppe G Abelsk hvis a∙b=b∙a for alle elementer a og b i G. Det betyr at det alltid finnes en entydig løsning av ax=b, dvs. x=b/a=b∙a-1.
Vi kan lage en multiplikasjonstabell for rotasjoner og speilinger i Dn. Klipp ut en liten papp-plate, helst med forskjellig farge på hver side, merk den med bokstaver og se at dette stemmer. Legg merke til at rotasjoner bevarer fargen på platen som vender mot deg, mens rotasjoner endrer fargen For to tilfeldige elementer i en gruppe finnes det en operasjon (kombinasjonsregel) som tilordner et entydig tredje element i gruppen.
Hvis vi lar utfallsrommet S være hjørnene i firkanten,
S={A,B,C,D} så kan disse hjørnene ordnes på 4! forskjellige måter, men det er bare 8 symmetrier.
Regulære mangekanter (polygoner)har like vinkler og like lange sider. Vi kan starte med en trekant, gå via firkant, femkant, sekskant osv. og når n går mot uendelig ender vi opp i en sirkel. En sirkel kan betraktes som et uendelig mangesidet polygon.

Det viser seg at en n-kant har 2n symmetrier, og for vår firkant (n=4) vil da få 8 symmetrier (4 rotasjoner + 4 speilinger). En trekant har 6 symmetrier R3={r1,r2,r3}={0o, 120o,240o}, og 3 speilinger om de 3 aksene, S3={s1,s2,s3}.
Gruppen SO3 er en fast kule som roterer rundt en akse gjennom origo.
Denne regningen kan videreutvikles ved å gå fra planet med to dimensjoner til romlige figurer i 3 dimensjoner som e.g. en kube:

Det finnes 5 regulære polyedere: tetraeder (4 liksidet trekanter), kuben eller terningen (6 kvadratiske flater), oktader (8 likesidete trekanter), dodekader (12 likesidete femkanter), ikosaeder (20 likesidete trekanter), og videre til n-dimensjonale vektorrom.
Vi skjønner raskt at Rubiks kube, utviklet av ungareren Ernõ Rubik, som i sin enkleste form er en 3x3x3 kube, i alt 27=3x3x3 småkuber som er hengslet slik at de kan dreies i flere plan, 7 fastsittende og 20 flyttbare med i alt 6 forskjellige farger, nå kan betraktes som en gruppe som det kan regnes med. Av de 20 flyttbare er det 8 hjørner med 3 synlige sider og farger, og 12 midtfelt med 2 synlige sider (farger). Hvert hjørne kan være på 8 forskjellige steder (8!) og hvert hjørne viser 3 av de i alt 6 mulige fargene. Det er 12 midtfelt (12!) som viser 2 av de 6 mulige fargene. I alt gir dette ca.4.3∙1019 mulige måter å plassere fargene.

Apropos store tall. En googol er et ettall etterfulgt av hundre nuller = 1∙10100 ≈ 70!
En googolplex er lik 10googol.
Eksempler på andre store tall:
Avogadros tall = 6.02214179∙1023 tilsvarer ett mol partikler, som er lik antall 12C-karbonatomer i 12 g karbon i grunntilstanden.
1 mol vann = 0.018 liter = Avogadros tall med vannmolekyler. Det skal ikke så veldige mange liter vann til før man skjønner at dette blir et vanvittig stort antall vannmolekyler med tilhørende statistisk fordeling når det gjelder kinetisk energi.
Vi sier at gruppen G er en gruppe hvis
1. For elementene x og y i G (kan finnes et element z slik at for alle x, y og z i G gjelder:
\(x \cdot(y\cdot z)=(x\cdot y)\cdot z\)
Dette er den assosiative loven.
2. Dessuten skal gruppen G inneholde ett og bare ett identitetselement e slik at for alle x gjelder:
\(x\cdot e=e\cdot x\)
3. Det skal være en invers av x kalt x-1 slik at:
\(x\cdot x^{-1}=x^{-1}\cdot x=e\)
Ethvert element i gruppen har et inverst element
Vi kan også definere undergrupper av G.
Eksempel på en gruppe er alle de relle tallene (R), samt de de rasjonale- (Q) og komplekse (C) tallene danner grupper, kropp (felt). Heltallene er ikke en kropp siden 1/2 ikke blir et heltall. Klammeparentes { } angir en mengde.
\(x \in G\)
betyr at x er et element i G, hvor ![]() angir medlemskap i en mengde.
angir medlemskap i en mengde.
Et kvadrat har rotasjons- og speilingssymmetri, vist foran, men et kvadrat har ikke translasjonssymmetri. Hvis et kvadrat flyttes fra et sted til et annet så ser vi at det blir forflyttet. Har vi imidlertid en uendelig flate dekket av kvadrater, så vil denne flaten ha translasjonssymmetri.
Roger Penrose studerte hvordan flater kan dekkes av fliser (tesselering). Noen av disse er ikke helt regulære og har ikke translasjonssymmetri.
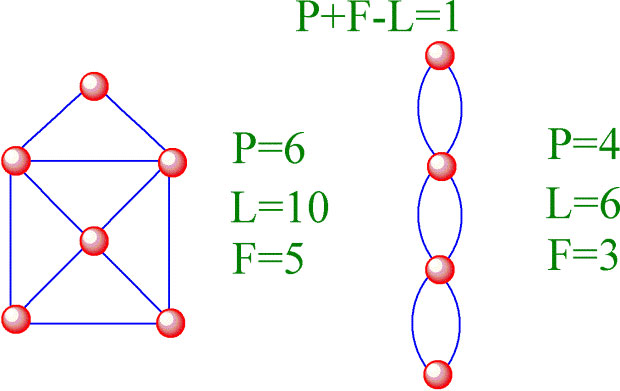
Eulers nettverksformel for punkter (P),linjer (L) og lukkete regioner (flater, F). Summen av punkter og regioner, minus antall linjer er lik 1:
\(P+F-L=1\)
Ringer og kropper
Kropp eller felt var det begrep som ble innført av Abel og Galois i arbeidet med å finne løsninger i polynomligninger med rasjonale koeffisienter med grad 5 eller høyere, det vil si femtegradsligninger, sjettegradsligninger osv.
Begrepene kropp og ring innen abstrakt algebra starter med Richard Dedekin, og blir videreført av Emmy Noether og Wolfgang Krull på 1920-tallet. Dedekin kalt en samling relle eller komplekse tall som er lukket under de fire regneoperasjonene (addisjon, subtraksjon, multiplikasjon, og divisjon) for Körper (kropp, corpus) og betegnes ofte K. Hilbert innførte begrepet Zahlring (tallring).

Også andre har gitt viktige bidrag til tallteori, slik som den indiske autodidakten Srinivasa Ramamujan (1887-1920), hvis talent ble oppdaget av den britiske matematikeren G. H. Hardy (1878-1948), e.g. taxitall.
En ring er en mengde R med to regneoperasjoner, addisjon (R,+) og multiplikasjon (R,∙), og slik at mengden danner en Abelsk gruppe. Vi kan se bort fra subtraksjon og divisjon siden disse bare er inverse av addisjon og multiplikasjon. For at R skal være en ring må flere aksiomer gjelde. Lukket under addisjon vil si at for alle a,b i R så må resultatet a+b også være i R.
(R,+) må være en Abelsk gruppe under addisjon med følgende aksiomer:
\(a+(b+c)=(a+b)+c\)
Det må eksistere et nullelement 0 i R slik at for alle elementene i R gjelder følgende:
\(a+0=0+a=a\)
0 er nullelementet og –a er den inverse slik at:
\(a+(-a)=0\)
For alle a og b i R gjelder:
\(a+b=b+a\)
De fire ovenforstående aksiomene gir en Abelsk gruppe under addisjon.
(R,∙) må være lukket under multiplikasjon, det vil si for alle a og b i R må også resultatet av regneoperasjonen a∙b være i R.
Den assosiative loven for multiplikasjon må gjelde med følgende aksiom:
\(a(bc)=(ab)c\)
Det må finnes et multiplikativt identitetselement 1 i R slik at
\(1\cdot a=a\cdot 1=a\)
Dessuten må de distributive lovene gjelde:
\(a(b+c)=ab+ac\)
\((a+b)c=ac+bc\)
Heltallene Z (…-3,-2,-1,0,1,2,3…) er eksempel på en ring, men de rasjonale tall Q og reelle tall R er også en ring. Z4 bestående av tallene {0,1,2,3} er en ring. For de rasjonale tall har vi divisjon slik at for alle elementer a ≠ 0 i Q så finnes det en multiplikativ invers:
\(\frac{1}{a}=a^{-1}\;\;\;\;\; aa^{-1}=1 \;\;\; a\neq 0\)
Alle aksiomene over gjelder for en kropp. Det betyr at de rasjonale tall Q, de reelle tallene R og de komplekse tallene Cer en kropp, men heltallene Z er ikke en kropp siden 1/2 er ikke et heltall.
Krystaller og rotasjonssymmetri
Krystaller omhandler hvordan materien organiserer seg selv. Krystaller kan bli beskrevet av krystallenheten, type krystallgitter og symmetri. Krystallgitteret gir syv krystallsystemer: monoklin, triklin, ortorombisk, trigonal, tetragonal, kubisk og heksagonal. Den funksjonelle enheten i en krystall kan angis av tre vektorer og vinklene mellom dem alfa (α) mellom b og c, beta (β) mellom a oc c og b gamma (γ mellom a og b. Skruaksen kan ha rotasjon 180o, 90o og 60o. x-akse (a), y-akse (c) og z-akse( b) kan rotasjonsaksene (symmetriaksene) 2, 3, 4 og 6, men ikke 5. Man finner aldri femkanter i en krystall. Å fylle et plan med femkanter (pentagoner) i tesseleringer umulig, men det er mulig med likesidete trekanter, firkanter og sekskanter. Det er heller ikke tredimensjonalt med dodekaeder med femsidete kanter. Diffraksjonsmønster i regulære krystaller har aldri fem-talls symmetri Krystallgittere og + symmetrier gir i alt 230 rom grupper.
Tidligere trodde man at alle krystaller hadde en repeterende (periodisk) struktur og at femtaltruktur ikke fantes, helt til man oppdaget kvasikrystaller. Kvasikrystaller er krystallignende , men har ikke noe repeterende mønser, de er ikke-periodiske og har ikke translasjonssymmetri. I kvasikrystaller er det ikke gjentak.
Den israelske kjemikeren og fysikeren Dan Shechtman (f.1941) fikk nobelprisen kjemi 2011 «for oppdagelsen av kvasikrystaller». Kvasikrystaller er ordnete strukturer, men som ikke er periodiske. Kvasikrystaller har diffraksjonsmønster som også har 5-talls symmetri, Roer penrose viste i 1974 at fliser i et plan kan ha både regularitet og femtallssymmetri. Penrose viste at med to forskjellige romber hvor hver av dem var vinkler som er multiplum av 36o, en rombe med vinkel 36o og 144o og den andre 72o og 108o.
Natur og kultur
Repetitio est mater studiorum. Gjentakelse er studienes mor.
Litteratur
Wikipedia