Vektorer innen biologi
Det binære vektorsysemet for T-DNA fra krongalle for transformasjon av planteceller. Ekspresjonsvektor hvor et plasmid blir brukt til å uttrykke et protein i en bakterie. Viral vektor er et virus brukt til å overføre et gen til en organisme. En shuttle-vektor benytter brukes til å spre informasjon via en organisme til en annen organisme
En spredningsvektor sprer en reproduktiv struktur e.g. insekter som sprer pollen.
Vektorer innen matematikk og fysikk
René Decartes (1596-1650) innførte begrepet analytisk geometri. I planet velges to koordinatakser som står vinkelrett på hverandre. En horisontal x-akse (abscisse) og en vertikal y-akse (ordinat) som møtes i et origo.
To tall (x,y) representerer et punkt i planet, et todimensjonalt rom, hvor x og y kalles koordinater. Koordinatene viser avstanden fra punktet til aksene. Tre tall (x,y,z) er en trippel og representerer et punkt i et tredimensjonalt rom, hvor z-aksen står rettvinklet på planet og alle tre aksene skjæres i origo. De tre tallene kan også skrives som (x1,x2,x3). (x1,x2,x3,x4) er en kvadruppel i et firedimensjonalt rom. (x1,x2,x3,…xn), n-tuppel, er et punkt i et n-dimensjonalt rom.
En overflate i et tredimensjonalt rom kan skrives som funksjonen:
\(f(x,y,z)=0\)
Derivere er å trekke tangenter til kurver, integrere er å beregne areal under kurver, og med partiellderiverte kan man studere kurver i rommet. Lagrange publiserte i 1788 Mécanique analytique (Analytisk mekanikk). Seinere innførte den irske matematikeren William Rowan Hamilton (1805-1865) Theory of quaternions, kvaternioner, en helt ny måte å forstå fysikk. I fysikk har man begreper som kraft, forflytning, hastighet og akselerasjon, alle disse har størrelse og retning og kan presenteres som en vektor. En vektor kan presenteres geometrisk fra et startpunkt til et sluttpunkt, eller analytisk via koordinatene for endepunktet.
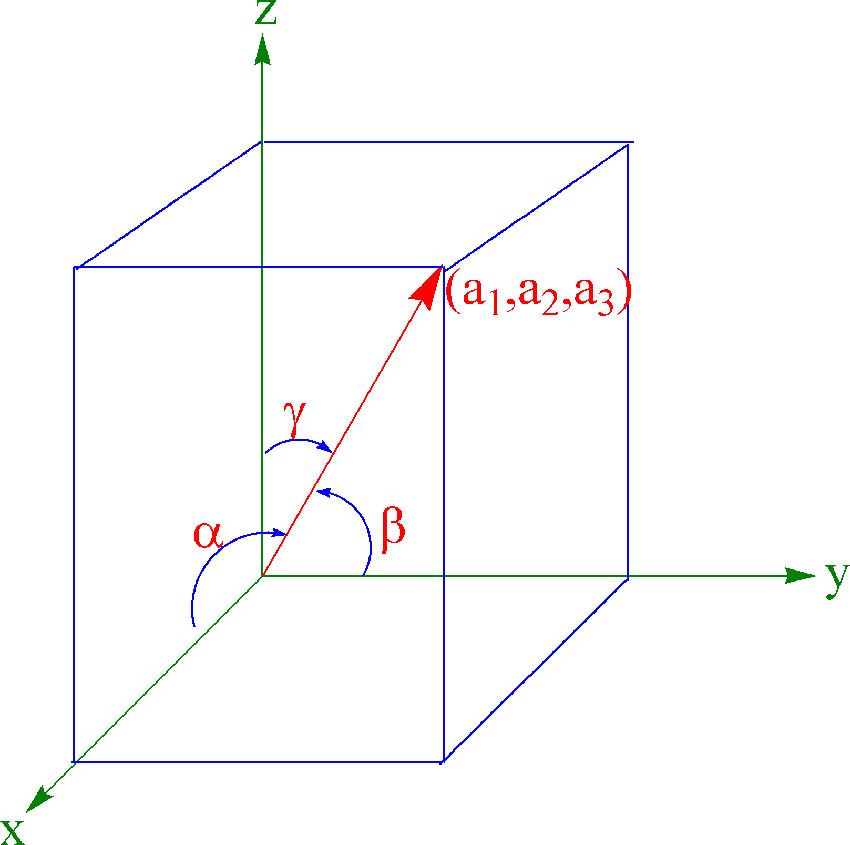
Vi har en vektor
\(\overrightarrow A= (a_1, a_2, a_3)\)
hvor a1, a2 og a3 er er komponentene til vektoren.
Vi har retningsvinklene til vektoren:
\(\cos \alpha= \frac{a_1}{|\overrightarrow A|}\;\;\;\;\;\; \cos \beta= \frac{a_2}{|\overrightarrow A|}\;\;\;\;\;\; \cos \gamma= \frac{a_3}{|\overrightarrow A|}\)
\(\cos ^2 \alpha + \cos^2 \beta + \cos^2 \gamma= 1 \)
Vektorsum
Vi har to vektorer A og B:
\(\overrightarrow A= (a_1, a_2, a_3, \dots, a_n)\;\;\;\;\;\; \overrightarrow B= (b_1, b_2, b_3, \dots, b_n)\)
Summen av de to vektorene A+B er lik:
\(\overrightarrow{A+B}= (a_1 + b_1, a_2 + b_2, a_3 + b_3, \dots, a_n + b_n)\)
Addisjon og multiplikasjon av todimensjonale vektorer kan vises geometrisk i planet. Summen er diagonalen i parallellogrammet dannet av de to vektorene A og B.
\(\overrightarrow A= (-1, 1)\;\;\;\;\, \overrightarrow B=(2,2)\;\;\;\;\; \overrightarrow{A+B}= (1,3)\)
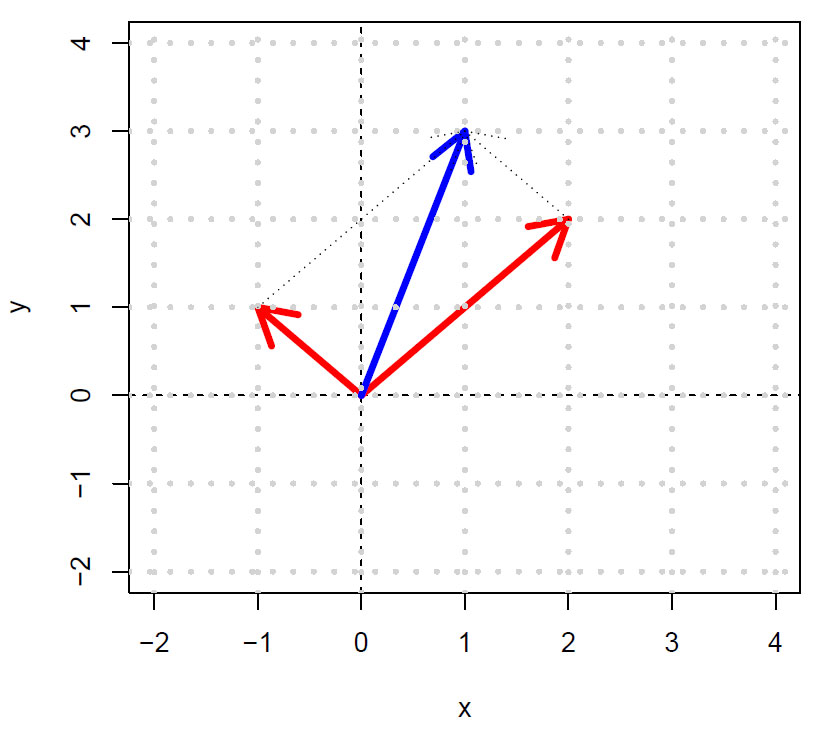
En vektorsum
Multiplikasjon av vektoren A med 2 dobler lengden, multiplikasjon med ½ halverer lengden. Generelt vil c∙A gi et punkt i samme retning som A, men c ganger avstanden. Hvis c er et negativt tall snur vektoren retning.
Determinanter kan brukes til å finne arealet av et parallellogram. Arealet er lik absoluttverdien til determinanten til vektorene A og B. Determinanten blir:
\(\begin{vmatrix} -1 & 2\\ 1& 2 \end{vmatrix}= -1 \cdot 2-1\cdot 2= -4\)
hvor absoluttverdien av determinanten blir lik 4 dvs. arealet blir lik 4. Dette kan vi kontrollregne ved å bruke Pytagoras setning.
Vektorprodukt
Absoluttverdien av vektorproduktet eller kyrssproduktet blir lik arealet A av parallelogrammet laget og utspent av de to vektorene:
\(A= | \overrightarrow A \times \overrightarrow B|\)
\(\overrightarrow A \times \overrightarrow B= \overrightarrow n\cdot |\overrightarrow A|\cdot |\overrightarrow B| \cdot \sin \theta\)
hvor theta er vinkelen mellom vektorene og \(\overrightarrow n= (i, j, k)\) er enhetsvektorer. Høyreregelen hvor pekefinger følger vektor A, langfinger (mellomfinger) følger regningen vektor B så følger vektorproduktet retningen på tommeltotten.
Vi må skille skalarprodukt fra vektorprodukt. Vektorprodukt vil si å finne en vektor som står normalt (vinkelrett) på to andre vektorer. Vi får vektorproduktet mellom to vektorer A og B lik A x B.
\(\overrightarrow A \times \overrightarrow B\)
Vektorproduktet kan peke opp eller ned. A x B har motsatt retning av B x A. Lengden av vektorproduktet A x B, hvis vi kaller vinkelen mellom vektorene A og B for α er
\(|\overrightarrow A||\overrightarrow B|\sin \alpha\)
Lengden av vektorproduktet A x B er lik arealet av et parallellogram bestemt av A og B, og som er lik absoluttverdien av determinanten. Vektorene A og B bør ligge i samme koordinatplan, enten xy-, xz- eller yz-planet slik at vektorproduktet peker ut i den tredje dimensjonen.
Hvis vektorene A og B ligger i xy-planet med koordinater:
\(\overrightarrow A= (x_1, y_1, 0) \;\;\;\;\; \overrightarrow B= (x_2, y_2, 0)\)
så blir vektorproduktet A x B lik:
\(\overrightarrow A \times \overrightarrow B = (x_1, y_ 1, 0) \times (x_2, y_2, 0)= \left( 0,0, \begin{vmatrix}x_1 & y_ 1\\ x_2 & y_ 2 \end{vmatrix} \right)\)
Vi kan finne vektorproduktet for A=[2,3,0] og B=[1,4,0], hvor absoluttverdien av determinanten blir lik 5:
\(\overrightarrow A \times \overrightarrow B = (2, 3, 0) \times (1, 4, 0)= \left[ 0,0, \begin{vmatrix}2 & 1\\ 3 & 4 \end{vmatrix} \right]= (0, 0, 5)\)
Hvis vi har basisvektorene eller enhetsvektorene i, j og k med lengde 1 i henholdsvis x-, y- og z-retning, så har vi generelt for vektorproduktet A x B hvor A=[x1,y1,z1) og B=[x2,y2,z2]
\(\overrightarrow A \times \overrightarrow B = (x_ 1, y_ 1, z_ 1 ) \times (x_2, y_ 2, z_ 2)= \begin {vmatrix} i & j & k \\ x_ 1 & y_ 1 & z_ 1\\ x_ 2 & y_ 2 & z_ 2 \end{vmatrix} \)
Vektorproduktet er velegnet til å finne arealer av trekanter og parallellogram dannet av vektorene i vektorproduktet.
Arealet av parallellogram er absoluttverdien av determinanten:
\(|\overrightarrow A \times \overrightarrow B|\)
Arealet av trekant:
\(\frac{1}{2}|\overrightarrow A \times \overrightarrow B|\)
På samme vis kan vi bestemme volumet av en parallellpiped dannet av tre vektorer A=[x1,y1,z1), B=[x2,y2,z2] C=[x3,y3,z3].
Volum av parallellpiped er lik absoluttverdien til determinanten:
\(\text{Volum av en parallelpiped}= \begin{vmatrix} x_1 & y_ 1 & z_ 1\\ x_2 & y_ 2 & z_ 2\\ x_3 & y_ 3 & z_3 \end{vmatrix}\)
Hvis vi har vektorene A=[4,3,2], B=[2,4,1] og C=[2,2,4] så blir volumet av parallellpiped dannet av de tre vektorene lik 30.
\(\begin{vmatrix} 4 & 3& 2\\ 2 & 4 & 1\\ 2& 2 & 4 \end{vmatrix}= 30\)
Hvis de tre vektorene A, B og C utgår fra samme punkt omslutter de en pyramide. Da vil volumet av pyramiden bli lik 1/3 av absoluttverdien til determinanten:
\(\text{Volum pyramide}= \frac{1}{3}\begin{vmatrix} x_1 & y_ 1 & z_ 1\\ x_2 & y_ 2 & z_ 2\\ x_3 & y_ 3 & z_3 \end{vmatrix}\)
Hvis de tre vektorene A, B og C er like lange og utgår fra samme punkt omslutter de et tetraeder. Da vil volumet av tetraederet bli lik 1/6 av absoluttverdien til determinanten:
\(\text{Volum tetraeder}= \frac{1}{6}\begin{vmatrix} x_1 & y_ 1 & z_ 1\\ x_2 & y_ 2 & z_ 2\\ x_3 & y_ 3 & z_3 \end{vmatrix}\)
Kulekoodinater
Funksjonen for en kule med radius r og sentrum i origo:
\(x^2 + y^2 + z^2 = r^2\)
En kule med origo i [x0,y0,z0]:
\((x- x_0) ^2 + (y-y_0) ^2 + (z- z_0) ^2= r^2\)
Vi kjenner kulekoordinatene (sfæriske koordinater) (u,v) til et punkt P(x,y,z) på en kule, hvor u tilsvarer breddegraden [-90o,90o] og v lengdegraden [0o,360o] på et kart. Hvis vi lar kula være Jorden så er meridianer storsirkler som går gjennom nord- og sydpol. Lengdegraden måles fra nullmeridianen og østover. For himmelkulen tilsvarer deklinasjonen breddegraden og rektascensjonen lengdegraden. Et punkt P0 i ekvatorialplanet har koordinater [x,y,0]. For Jorden med sentrum i origo og radius r =6378 km får koordinatene for et punkt P=[x,y,z]:
\(x= r \cos v\cos u\;\;\;\;\;\; y= r \cos v\sin u\;\;\;\;\;\; z= r \sin v\)
\(\tan u= \frac{y}{x}\;\;\;\;\;\, \sin v= \frac{z}{r}\)
Hvis en kule har sentrum i [x0,y0,z0] så blir parameterfremstillingen:
\(x=x_0 + r \cos v\cos u\;\;\;\;\;\; y= y_0 + r \cos v\sin u\;\;\;\;\;\; z= z_0 + r \sin v\)
Skalarprodukt (prikkprodukt)
Vi innfører en ny type multiplisering hvor skalarproduktet gir et reelt tall. Skalarproduktet A∙B av to vektorer avbildes som en skalar:
\(\overrightarrow A \cdot \overrightarrow B= (a_1 \cdot b_1 + a_2 \cdot b_2+ a_3 \cdot b_3+ \dots, +a_n \cdot b_n)= \displaystyle\sum_ {k= 1}^n a_k \cdot b_k\)
Skalarproduktet av en vektor med seg selv er kvadratet av lengden av vektoren:
\(\overrightarrow A \cdot \overrightarrow A= |A|^2\)
Skalarproduktet av to vektorer er lik produktet av lengden av de to vektorene multiplisert med cosinus til vinkelen θ mellom dem:
\(\overrightarrow A \cdot \overrightarrow B=\parallel A \parallel \cdot \parallel B \parallel \cos \theta\)
Vet vi lengden og skalarproduktet kan vi finne vinkelen mellom to vektorer.
\(\cos \theta= \displaystyle\frac{\overrightarrow A \cdot \overrightarrow B}{|\overrightarrow A| \cdot |\overrightarrow B|}= \frac{a_1 b_1 + a_2 b_2 + a_3 b_ 3}{\sqrt{a_1 ^2+ a_2 ^2+a_3 ^2}\cdot \sqrt{b_ 1 ^2 + b_ 2 ^2 + b_ 3 ^2}}\)
Vi har at:
\(\overrightarrow A \cdot \overrightarrow B= \overrightarrow B \cdot \overrightarrow A\)
Hvis de to vektorene A og B står normalt på hverandre blir
\(\overrightarrow A \cdot \overrightarrow B = 0\)
fordi cosθ=0. Vi sier at nullvektoren står normalt på alle vektorer. Ortogonale vektorer står på hverandre i 90o vinkel. Hvis nullvektoren er A=0 så er:
\(\overrightarrow A \cdot \overrightarrow A = 0\)
Vi kan finne vinkelen mellom to vektorer A=[1,-1,0] og B=[1,0,1]
\(\cos \theta= \displaystyle \frac{1 + 1 + 1}{\sqrt{1+1 } \cdot \sqrt{1+1 }}= \frac{1}{\sqrt{4}}= \frac{1}{2}\)
Skalarproduktet er svært nyttig i fysikk hvor vektoren A kan representere en konstant kraft som virker på et legeme som beveger seg som en vektor B. Arbeidet som utføres blir lik skalarproduktet A∙B
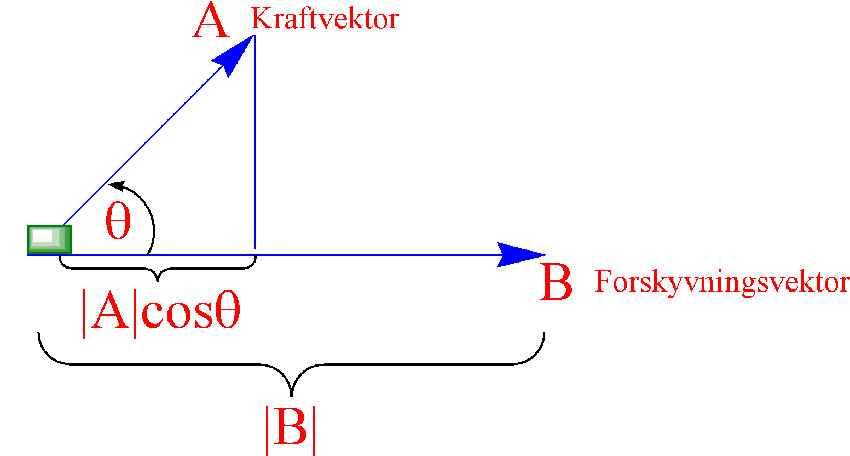
Hvis c er et tall så vil c∙A bli:
\(c\cdot \overrightarrow A= (c\cdot a_1 , c \cdot a_ 2, c \cdot a_ 3, \dots, c \cdot a_n)\)
Lengden eller normen til en vektor er :
\(|\overrightarrow A|= \sqrt{\overrightarrow A \cdot \overrightarrow A}= \sqrt{a_ 1 ^2+a_ 2 ^2 + a_ 3 ^2 + \dots + a_n ^2}\)
Hvis A og B er to vektorer så gjelder trekantulikheten:
\(|\overrightarrow A+ \overrightarrow B| \leq |\overrightarrow A| + |\overrightarrow B|\)
I det tredimensjonale rommet er det tre enhetskoordinatvektorer i=[1,0,0], j=[0,1,0], og k=[0,0,1] alle med lengde 1, og som ligger langs x-,y- og z-aksen. Vektorene i, j og k danner basis i det tredimensjonale rommet 3D (R3):
Alle vektorer kan uttrykkes i form av enhetsvektorene:
\(\overrightarrow A = a_ 1 \cdot \overrightarrow i + a_ 2 \cdot \overrightarrow j + a_ 3 \cdot \overrightarrow k\)
Hvis det er samme lengdeakse på aksene kalles koordinatsystemet ortonormert.
Bevegelse kan beskrives av posisjon (P(x,y,z), forflytning, hastighet (v=dx/dt) og aksellerasjon (a=dv/dt), og i denne sammenheng benytter vi vektorer.
En rett linje i et tredimensjonalt rom (R3)som går gjennom punktet P0(x0,y0,z0)og har retningsvektor (a,b,c) kan framstilles i parameterform som:
\(\begin{bmatrix} x= x_0 + at\\ y= y_0 + bt\\ z= z_0 + ct \end{bmatrix}\)
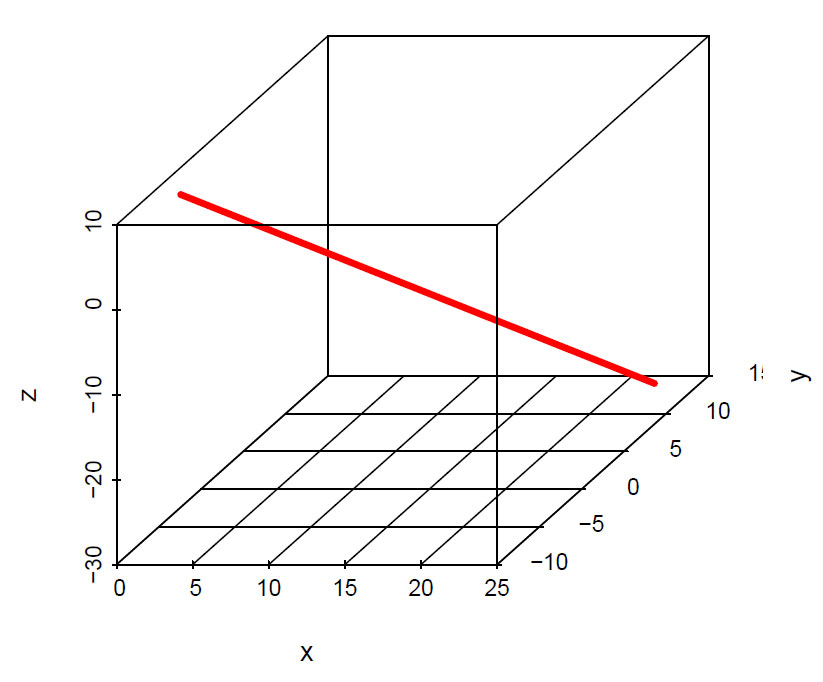
Vi plotter en linje som har parameterframstilling:
\(\begin{bmatrix} x = 2 + 2t\\ y= -6 + 2t\\ z= 10-4t \end{bmatrix}\)
Vi kan finne vinkelen mellom to linjer i rommet ved å finne vinkelen mellom retningsvektorene.
\(\begin{bmatrix} x = 2 + 2t\\ y= -6 + 2t\\ z= 10-4t \end{bmatrix}\;\;\;\;\; \begin{bmatrix} x = 2 - 2t\\ y= 4 + t\\ z= 5+2t \end{bmatrix} \)
Disse linjene har retningsvektorer r1(2,2,-4) og r2(-2,1,2).
Vi kan finne lengden av retningsvektorene |r1| og |r2|, skalarproduktet, cosinus til vinkelen, og vinkelen.