\(f(x)= a_0 + a_1x+ a_2x^2 + a_3 x^3 + \dots + a_nx^n\)
Og går mot pluss uendelig (∞) eller minus uendelig (-∞) når x går mot uendelig, avhengig av om an er større eller lik 0:
\(\lim\limits_{x \to \infty}f(x)= \begin{cases} \infty & \quad \text{hvis} \;a_n>0\\ -\infty & \quad \text{hvis }\; a_n<0 \end{cases} \)
Kvadratiske funksjoner
På begynnelsen av 1500-tallet i Italia forsøkte man å finne eksakte løsninger av ligninger for eksempel andregradsligninger (kvadratiske funksjoner) er av typen:
\(ax^2 + bx + c=0\)
som vi nå vet har følgende løsninger, røtter i form av rotuttrykk:
\(x=\displaystyle\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)
Vi ser på fortegnet for b2-4ac som også kalles diskriminanten til kvadratiske ligningen.
\(b^2 - 4ac \begin{cases} <0 & \quad \text{to løsninger }\\ =0 & \quad \text{en løsning}\\ <0 & \quad \text{ingen reelle løsninger} \end{cases} \)
Hvis vi lar koeffisientene a,b og c være i feltet F og røttene i funksjonen f(x) er lik r1 og r2 så finnes det symmetriske rasjonale funksjoner hvor a=-(r1+r2) og b=r1∙r2
Alle polynomer skal ha en løsning, og man endte ut i vanskeligheter. Euler viste at hvis vi har ligningen:
\(x^2 + 1=0 \;\;\;\;\; \implies\;\;\; x=\pm \sqrt{-1}\)
så blir røttene ± kvadratroten til ±1. Dette var en type ligninger som i begynnelsen virket absurde, på lignende måte som cos(x)=2 eller ex=-1.
Euler løste dette i innføringen av komplekse tall og sette :
\(i= \sqrt{-1}\)
Vi kan se nærmere på ligninger av typen:
\(x^n - 1 =0\)
For:
\(x^2 - 1=0\;\;\;\;\;\; \implies \;\;\;\; x= \pm \sqrt{1}\)
Euler fant at for for n=3 er det tre røtter:
\(x^3 - 1=\left(x-1\right)\left(x^2 +x+1\right)=0\)
x=1 og de to andre finner man fra formelen for kvadratiske røtter:
\(x=\frac{-1\pm \sqrt{-3}}{2}\)
For:
\(x^4 - 1=0\)
er røttene:
\(1,\; -1,\; \sqrt{-1}, \; -\sqrt{-1}\)
For n=5 er det fire imaginære røtter i tillegg til 1.
Generelt har vi:
\(\cos \theta^2 + \sin \theta^2 = 1\)
Denne kan faktoriseres:
\(\cos \theta^2 + \sin \theta^2 = 1=\left(\cos\theta + i\sin \theta\right)\left(\cos \theta + i\sin \theta\right)\)
Som fører fram til De Moivres teorem (Abraham De Moivre 1667-1754):
\(\left(\cos \theta + i \sin\theta\right)^n= \cos(n\theta) + i \sin (n\theta)\;\;\;\; \text{for} \ n\geq1\)
Generelt vil ligningen:
\(x^n - 1 =0\)
dele opp en sirkel med n komplekse røtter:
\(\cos \frac{2\pi k}{n }+i \sin \frac{2\pi k}{n }\;\;\;\;\; \text{for}\;\; k= 0, 1, 2, 3, \dots,n-1\)
og de komplekse røttene blir liggende på enhetssirkelen i kompleksplanet, her for n=50
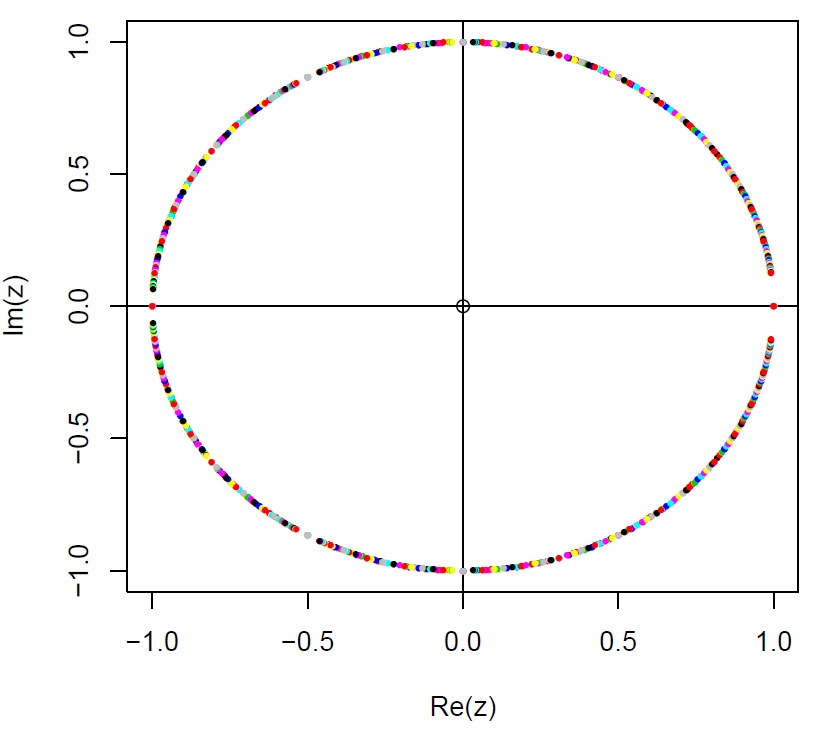
Løsningene for xn-1=0 for n=50 blir liggende på enhetssirkelen i kompleksplanet med reell akse Re(z) og imaginær akse Im(z).
Vi kan se på kvadratligningen:
\(f(x)=x^2-4x+1\)
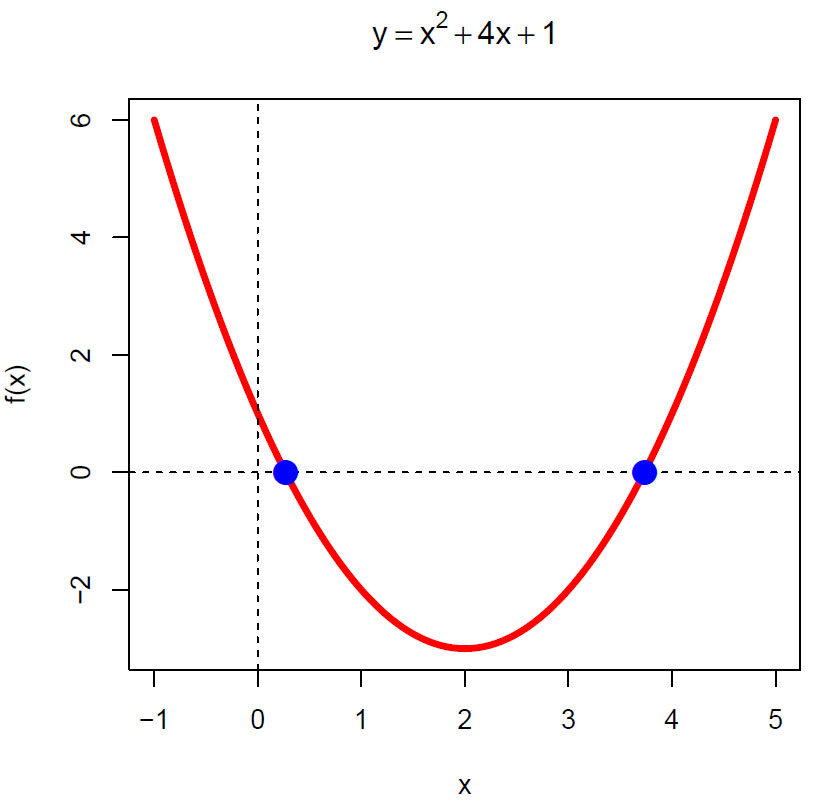
Vi finner røttene ved å sette inn i uttrykket over:
r1= 3.7320499 og r2= 0.2679501
Vi kan lage algebraiske funksjoner av røttene:
\(r_1+r_2 = 4\;\;\;\;\;\; r_1\cdot r_2=1\)
Galoisgruppen til f(x) er to permutasjoner.
En spesiell ligning er:
\(f(x)= x^2 + x+ 41\)
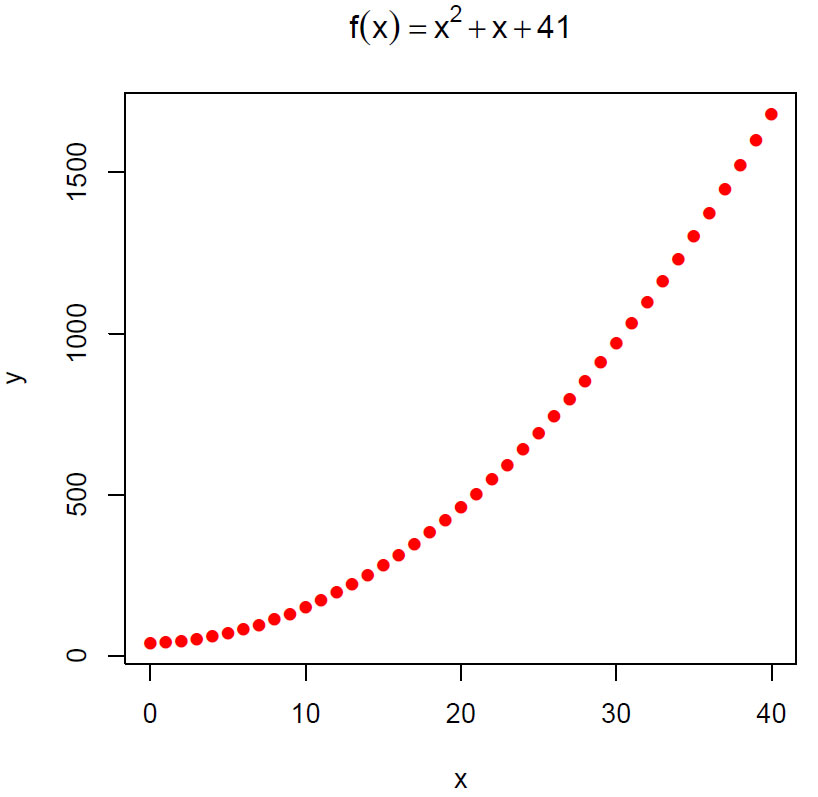
hvor resultatet av f(x) blir mange primtall for x=[0,39]
41 43 47 53 61 71 83 97 113 131 151 173 197 223 251 281 313 347 383 421 461 503 547 593 641 691 743 797 853 911 971 1033 1097 1163 1231 1301 1373 1447 1523 1601
For ligningen over er a=1,b=1 og c=41, dvs. b2-4ac=1-164=-163 og det blir to komplekse røtter:
\(x= -\frac{1}{2} \pm\frac{1}{2}\sqrt{-163}\)
Tallet 163 har spesielle egenskaper.
Vi har sett at andregradsligninger har løsninger med rottegn og tredjegradsligninger har også slike løsninger:
\(f(x)= ax^3 + bx^2 + cx+ d\)
gjengitt av Girolama Cardano i Ars Magna (1545). Fjerdegradsligningen kan reduseres til 2 andregradsligninger. Kvintligningen (femtegradsløsningen) ble undersøkt av Niels Henrik Abel i 1824. En symmetrigruppe med fem elementer er ikke løsbar og derfor kan ikke en femtegradsligning løses ved rotutrykk.
Kubiske funksjoner (tredjegradspolynomer)
Et kvadratisk polynom av typen:
\(f(x)= \beta_0+ \beta_1 x + \beta_2 x^2\)
Et kubisk polynom blir:
\(f(x)= \beta_0+ \beta_1 x + \beta_2 x^2 + \beta_3 x^3\)
Generelt er en kubisk funksjon (tredjegradspolynom, tredjegradsligning) følgende:
\(f(x)= ax^3 + bx^2 + cx + d\)
hvor a, b, c og d er reelle tall.
Vi har sett at andregradsligninger har løsninger med rottegn og tredjegradsligninger har også slike løsninger, gjengitt av Girolama Cardano i Ars Magna (1545).
Vi finner røttene til funksjonen ved f(x)=0.
\(f(x)= ax^3 + bx^2 + cx + d= 0 \;\;\;\;\, a \neq 0\)
Kubiske funksjoner med reelle koeffisienter har minst en løsning som er reell.
Den deriverte av en kubisk funksjon blir en kvadratisk funksjon (andregradspolynom):
\(f'(x)= 3ax^2 + 2bx + c\)
Integralet av den kubiske funksjonen blir et kvartfunksjon (fjerdegradspolynom.
Kubiske funksjoner var allerede kjent i det gamle Babylonia, Egypt, India, Persia, Kina og i Grekenland (Diofantus, Arkimedes)
Eksempel 1
Vi ser på funksjonen:
\(f(x)= x^3 - 6x-4\)
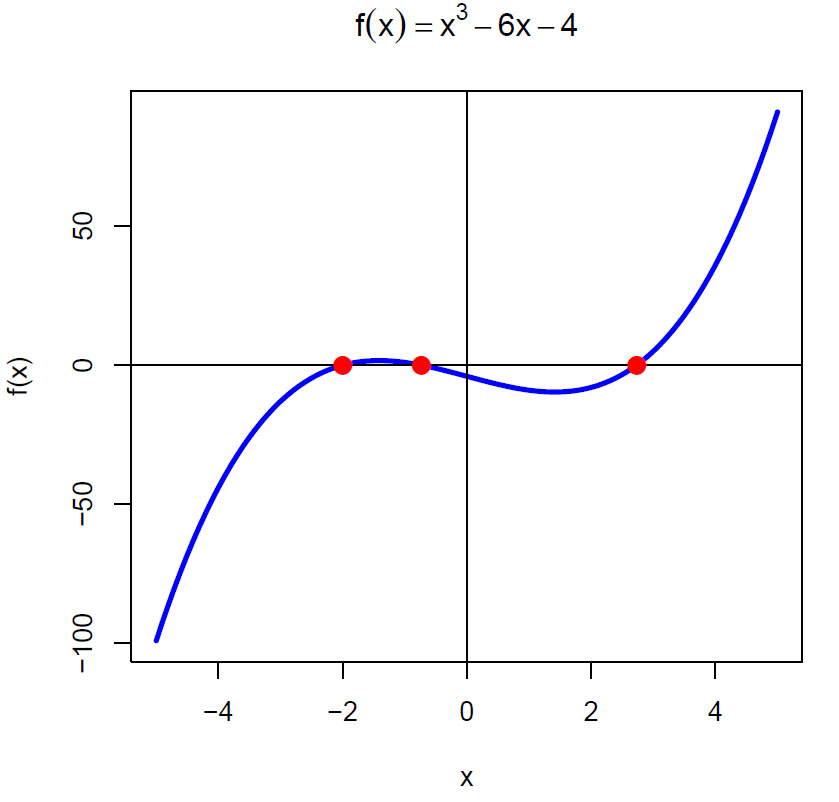
Ligningen y=x3-6x-4 har to negative og en positiv løsning (røtter), numerisk løsninger -2.0000000, -0.7320684, og 2.7320518.
Eksempel 2
Vi skal studere funksjonen:
\(f(x)= x^3 - 12x + 1\)
Vi skal finne maksimumspunktene med kommandoen optimize() og sammenligne med å finne den førstederiverte og finne røttene i den førstederiverte:
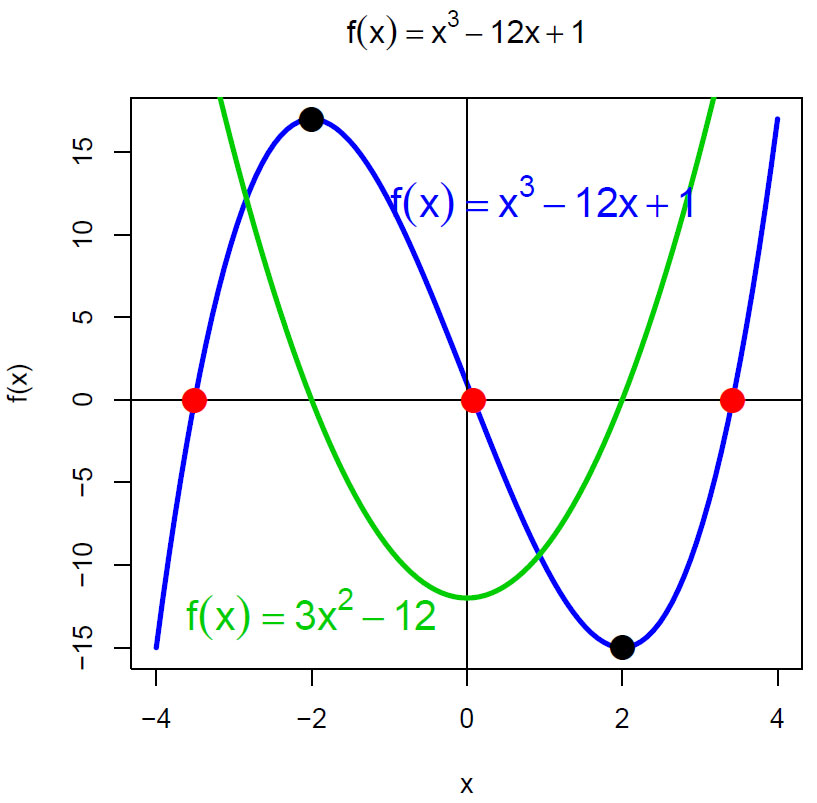
Tredjegradspolynom x3 -12x+1 med røttene -3.50503709 , 0.08338865 og 3.42165396og funksjonen for den deriverte f'(x) lik 2x^2 - 12 med røttene -2 og 2
Vi ser at den førstederiverte er lik 0 ved maks-, og min-punktene for funksjonen.
Eksempel 3
Vi skal studere den kubiske funksjonen:
\(f(x)= x^3 -2x^2- 3x+2\)
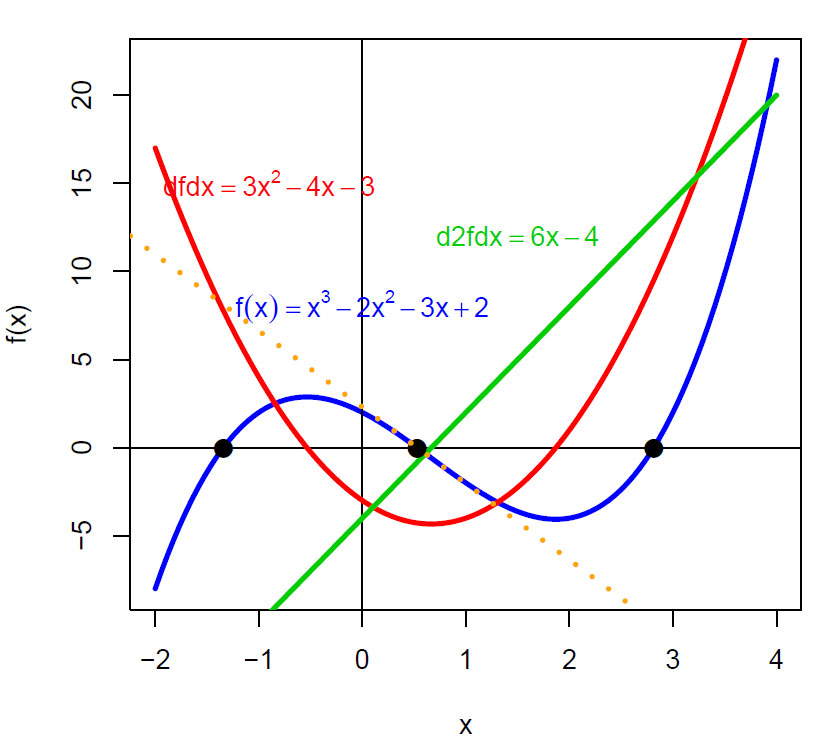
Den kubiske funksjonen f(x)= x3 -2x2-3x+2 (blå) med røttene -1.3429231, 0.5293368 og 2.8136067, den førstederiverte f'(x)= 3x2 -4x-3 (rød) og den andrederiverte f''(x)= 6x-4 (grønn linje). Vendetangenten som en prikket linje.
Eksempel 4
Vi har gitt en kubisk funksjon:
\(\displaystyle f(x)=- \frac{x^3}{3}+ 2x^2+ 4x-6\)
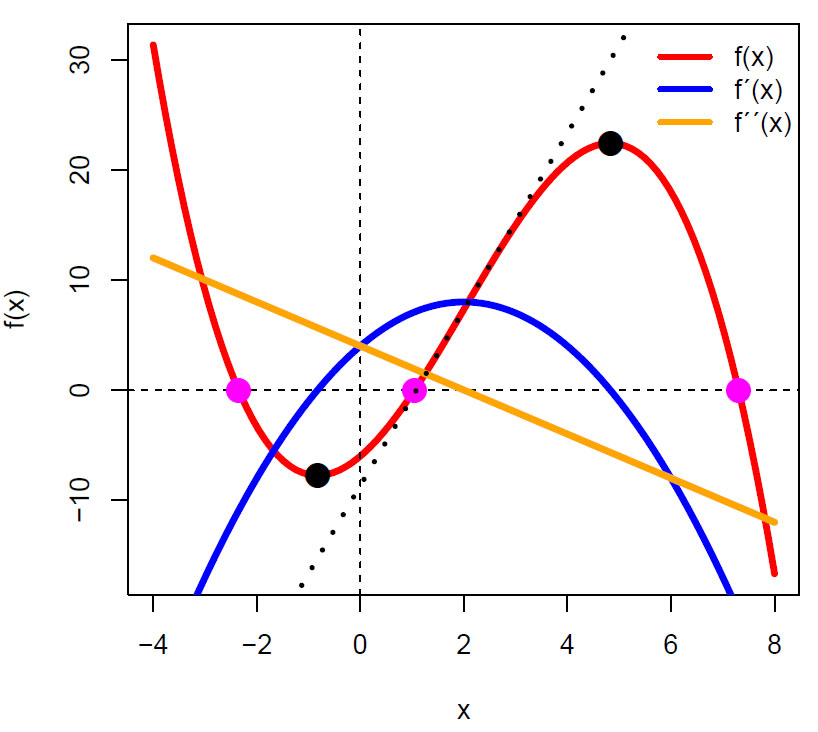
Funksjonen f(x) (rød)= -x3/3 + 2x2+4x-6, den førstederiverte f'(x) (blå), den andrederiverte f''(x) (oransje rett linje), samt vendetangent (sort prikket) . Vi ser at den førstederiverte er lik 0 ved maksimums- og minimumspunktene til funksjonen (svarte punkter). Røttene til funksjonen f(x) er de fiolette punktene.
En deriverbar funksjon y=f(x) kan ha kritiske punkter hvor den førstederiverte er lik null f’(x)=0, i form av maksimums- eller minimumspunkter, lokale eller globale. Når man skal finne maksimums- og minimumspunkter for en funksjon f(x)med en variabel finnes først punktene for den førstederiverte av funksjonen er lik 0 (f’(x)=0). For å avgjøre hvem av dem som er maksimum og minimum benyttes den andrederiverte f’’(x). Vi har et lokalt minimum når f’’(x)>0 og et lokalt maksimum når f’’(x)<0. Hvis f’’(x)=0 kan man ikke trekke noen slutning.
Når den førstederiverte er større enn 0, f’(x)>0 stiger kurven og når den førstederiverte er mindre enn 0, f’(x)<0 synker kurven. Vendepunkt er der kurven skifter mellom å stige og synke.
Historie
Algebra har sitt navn etter arabiske læreboken Algebr wal muqababla (Gjenopprettelse og forenkling av ligninger) skrevet av Mohamed Ibn Musa Al-Khwarizimi. 820 e.kr., som forener arabisk, gresk og indisk algebra. Kunnskapen blir seinere overført til Italia. Løsning av andregradsligninger var allerede kjent fra Babylonia.
Publiseringen av løsningen av kubiske ligninger er en berømt historie fra vitenskapen i renessansen. Det var den italienske matematikeren Scipione del Ferro (1465-1526), professor i geometrisk algebra ved universitetet i Bologna, som utviklet en metode for å finne røttene til kubiske funksjoner. Oppdagelsen holdt han hemmelig, men overlot den til sin student Antonio Maria Fiore. Var man professor måtte man vise sin kompetanse, og man kunne bli utfordret. Niccolò Fontana Tartaglia (1500-1577) hevdet han hadde funnet en løsningsmetode for tredjegradsligninger og kom i disputt med Fiore hvor det endte i konkurranse mellom dem om en pengepremie. Hver av dem skulle bidra til pengepremien, og hver av dem skulle gi den andre et problem som skulle løses. Fiore laget spørsmålet om løsning av, en kube + noe er lik et tall
\(x^3 + mx=n\)
og Tartaglia laget spørsmålet om:
\(x^3+mx^2 =n\)
til Fiore. Tartaglia vant. Tartaglia holdt fremdeles måten å løse på hemmelig, men røpet den for Gerolamo Cardano (1501-1576) under forutsetning av at Cardano skulle fortsette å holde det hemmelig, og hvis han skulle skrive en bok om kubiske ligninger skulle Tartaglia få beskjed slik at han kunne rekke å publisere. Cardano ble kjent med hva Ferro hadde funnet, og valgte å publisere løsningen i Ars Magna 1545, med argument at det var Ferros metode som ble vist. Det ble ny duell, Cardano ville ikke stille opp mot Tartaglia, men sendte sin student Lodovico Ferrari (1522-1565) som til slutt vant over Tartaglia. Ferrari bidro til løsningen av fjerdegradsligninger, måtte gå veien om tredjegradsligninger, men også dette ble publisert i Ars Magna. Cardano var også interessert i spill og gambling og skrev i 1526 Liber de ludo aleae (Bok om spill og tilfeldighet).
Euler kunne vise at løsningen på en ligning av typen:
\(x^3=mx+n\)
har løsningen:
\(x = ^3 \displaystyle \sqrt{\frac{n}{2}+ {\sqrt{\frac{n^2}{4}- \frac{m^3}{27}}+^3 \sqrt{\frac{n}{2}-\sqrt{\frac{n^2}{4}- \frac{m^3}{27}}}}}\)
Joseph Louis Lagrange publiserte i 1770 Réflextions sur la résolution algébrique des équations en metode som fungerte for tredje- og fjerdegradsligninger. Han analyserte ligningene til Cardano og Ferrari ved å betrakte dem som permutasjoner av røtter, men fikk det ikke til å virke for femtegradsligninger. Niels Henrik Abel kunne vise at det var umulig å løse generelle femtegradsligninger med vanlig rotuttrykk (Abel-Ruffiniteoremet).

Imidlertid finnes det noen femtegradsligninger som er løsbare som
\(\left(x-1\right)^5= 0\)
Hvorfor det finnes noen femtegradspolynomer og polynomer av høyere orden som er løsbare kunne Évariste Galois vise ved Galois-grupper (permutasjonsgrupper). Galois-teori viser symmetrien i røttene til n-tegradspolynomer.

Kvartfunksjoner
Kvartfunksjoner (fjerdegradsligninger) er av følgende type:
\(f(x)= ax^4 + bx^3 + cx^2 + dx + e\)
Fjerdegradsligningen kan reduseres til 2 andregradsligninger. Kvintligningen (femtegradsløsningen) ble undersøkt av Niels Henrik Abel i 1824. En symmetrigruppe med fem elementer er ikke løsbar og derfor kan ikke en femtegradsligning løses ved rotutrykk.
Dette er den høyeste orden av funksjoner som kan løses med rotuttrykk. Galois-teori med kobling mellom gruppeteori og feltteori viser hvorfor det må være slik. Koeffisientene a,b,c,d og e er i feltet F. Det som er avgjørende er om Galoisgruppen (permutasjonsgruppen) er løsbar eller ikke. Galois fant at røttene i en ligning kan beskrives av en algebraisk ligning, og at røttene kan omstokkes (permuteres). Galois startet med å studere symmetriske funksjoner. I moderne termer er det lettere å vise dette ved feltteori. Et algebraisk felt er en lukket gruppe av tall, for eksempel de rasjonale tallene, ved de vanlige regneoperasjonene addisjon, subtraksjon, multiplikasjon og divisjon. Heltallene danner ikke et felt fordi deling av et heltall med et annet heltall ikke nødvendigvis gir et heltall. Det kan foretas utvidelser av et felt og en-til-en avbildninger (automorfi) slik at egenskapene til addisjon og multiplikasjon bevares.
Grunnlaget for Galois-grupper er videreutviklet av Emil Artin (1898-1962) (artins resiprositetssats) bl.a. basert på arbeid til Julius Wilhelm Richard Dedekind (1831-1916),kjent for dedekinske snitt og idealteori og Emmy Amalie Noether (1882-1935). Universitetet i Göttingen hindret i starten at Emmy Noether skulle få undervise. I 1933 flyktet hun til USA grunnet nazistenes raselover. Emmy Noether har gitt viktige bidrag innen abstrakt albegra og teoretisk fysikk. Noethers teorem innen teoretisk fysikk kobler symmetri og bevaringslover.

Faktorisering av polynomer
Første kvadratsetning:
\(\displaystyle (a+b) ^2= a^2 + 2ab + b^2\)
Andre kvadratsetning
\(\displaystyle (a-b) ^2= a^2 - 2ab + b^2\)
Tredje kvadratsetning:
\(\displaystyle (a+b)(a-b)= a^2 - b^2\)
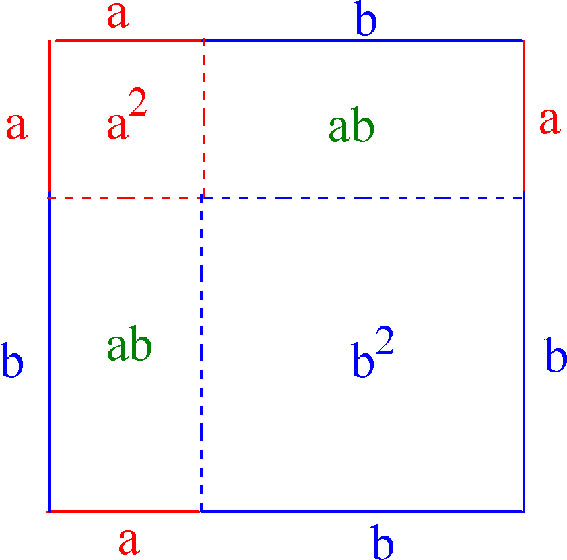
Vi kan faktorisere andregradspolynomer ved å bruke kvadratsetningene eller ved å finne røttene. Et n-tegradspolynom kan ikke ha flere enn n røtter (løsninger). Et andregradspolynom med røtter x1 og x2 kan faktoriseres som:
\(\displaystyle ax^2 + bx + c= a(x-x_1)(x-x_ 2)\)
Hvis andregradspolynomet bare har en rot blir faktoriseringen:
\(\displaystyle ax^2 + bx + c= a(x-x_1)(x-x_ 1)= a(x-x_1)^2\)
Vi finner nullpunktene til et andregradspolynom:
\(\displaystyle ax^2 + bx + c\)
\(\displaystyle x= \frac{-b\pm \sqrt{b^2 - 4ac}}{2a}\)
Vi kan faktorisere polynomet ved hjelp av røttene:
\(\displaystyle -3x^2-9x-6= -3(x+1)(x+2)\)
Vi kan faktorisere n-te gradspolynomer med røttene x1, x2, x3,….som:
\(\displaystyle a(x-x_1)(x-x_2)(x-x_3)\dots (x-x_n)\)
\(\displaystyle x^3-6x^2+11x-6= (x-1)(x-2)(x-3)\)
Litteratur
Adams, R.A. Calculus (4.ed.). Addison-Wesley 1999.
Apostol, T.M. Calculus (Vol I + II). Blaisdell Publ. Comp. 1962.
R Development Core Team (2011). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0, URL http://www.R-project.org/.
Rottmann, Karl: Matematische Formelsammlung. Bibliographisces Insitutt. Hochschultaschenbücher-Verlag. 1960.