Typer funksjoner
Hyperbolske funksjoner;;trigonometriske funksjoner;; polynomfunksjoner;; parabel;; periodiske funksjoner;; ;rett linje;;;
Når en 3D kuleflate skal projiseres ned i et 2D plan er dette en avbildning. Vi har en entydig avbildning hvis det til ethvert element i X finnes bare et element i Y. Vi har en invers avbildning hvis vi kan avbilde begge veier, dvs. vi har også f-1:Y→X og ff-1=1.
Funksjonen f(x)=ex (eksponentialfunksjonen) har den inverse logartimefunksjonen g(x)=ln(x)
\(y= e^x \;\;\;\;\, \iff\;\;\; y= \ln x\)
Når man skal finne maksimums- og minimumspunkter for en funksjon f(x)med en variabel finnes først punktene for den førstederiverte av funksjonen er lik 0 (f’(x)=0). For å avgjøre hvem av dem som er maksimum og minimum benyttes gen andrederiverte f’’(x). Vi har et lokalt minimum når f’’(x)>0 og et lokalt maksimum når f’’(x)<0. Hvis f’’(x)=0 kan man ikke trekke noen slutning.
I en todimensjonal figur har man et aksesystem med en horisontal linje kalt x-akse og en vertikal akse kalt y-akse. Der disse to aksene skjærer hverandre har man origo (0). Ethvert punkt i dette planet (xy-planet) kan angis med et par med tall (x,y) kalt koordinater, hvor x-koordinaten ofte kalles abscisse og y-koordinaten kalles ordinat.
Leibniz introduserte ordet funksjon om en type matematiske formler. Disse funksjonene kan tegnes som en grafisk framstilling i et plan med x- og y-koordinater. Sinus (sin), cosinus (cos) og tangens (tan) er eksempler på trigonometriske funksjoner som spesielle periodiske egenskaper. Studerer man tidsavhengige prosesser er x-aksen en tidsakse med tidsenheter t og tidsfunksjonen blir av typen f(t). Vi skal etter hvert se at prosesser som endrer seg over tid kan beskrives med differensialligninger. Dynamiske systemer, systemer som endrer seg over tid og/eller rom, kan beskrives i form av differensialligninger som har en kontinuerlig tidsakse, eller i form av differensligninger som er basert på iterasjoner (gjentakelse) og har en diskontinuerlig (diskret) tidsakse.
Funksjonsdrøfting
En deriverbar funksjon y=f(x) kan ha kritiske punkter hvor den førstederiverte er lik null f’(x)=0, i form av maksimums- eller minimumspunkter, lokale eller globale. Når man skal finne maksimums- og minimumspunkter for en funksjon f(x)med en variabel finnes først punktene for den førstederiverte av funksjonen er lik 0 (f’(x)=0). For å avgjøre hvem av dem som er maksimum og minimum benyttes den andrederiverte f’’(x). Vi har et lokalt minimum når f’’(x)>0 og et lokalt maksimum når f’’(x)<0. Hvis f’’(x)=0 kan man ikke trekke noen slutning.
Når den førstederiverte er større enn 0, f’(x)>0 stiger kurven og når den førstederiverte er mindre enn 0, f’(x)<0 synker kurven. Vendepunkt er der kurven skifter mellom å stige og synke.
Vi ønsker også å kunne finne maksimums- og minimums- og sadelpunkter hvis vi har flere variable. En måte å gjøre dette på er Lagranges multiplikator.
Lagranges multiplikatormetode (Joseph-Louis Lagrange 1736-1813) kan benyttes til å finne maksimums- og minimumspunkter for funksjoner. Hvis vi har to funksjoner f(x,y) og g(x,y) som har et berøringspunkt (x0,y0), så vil de partiellderiverte være proporsjonale i berøringspunktet og det finnes en Lagrange multiplikator lambda (λ) slik at
\(\displaystyle\frac{\partial f}{\partial x}= \lambda \frac{\partial g}{\partial x}\)
\(\displaystyle\frac{\partial f}{\partial y}= \lambda \frac{\partial g}{\partial y}\)

Lagranges multiplikatormetode kan hjelpe oss i å løse dette problemet, oppkalt etter den berømte franske matematikeren Joseph-Louis Lagrange (1736-1813). Generelt er problemet å finne ekstremalverdiene for en funksjon f(x,y,z), eller i vårt tilfelle f(x,y,a). Hvis z kan uttrykkes som en funksjon av x og y, z=h(x,y) så består problemet i å finne maksimum av en ny funksjon F(x,y)=f(x,y,h(x,y). Imidlertid er det ikke sikkert at z kan uttrykkes som funksjon av x og y. Maksimumspunktet ligger på en kurve C som kan tenkes angitt som skjæring mellom to flater g1(x,y,z)=0 og g2(x,y,z)=0. Hvis vi lar t være en parameter som beveger seg langs kurven C hvor vi skal finne maksimum blir problemet nå forenklet til F(t)=f(x,y,z), og maksimumspunktet må finnes der hvor den førstederiverte er lik 0. F’(t)=0.
Vi har nå tre skalarligninger som må løses hvor konstantene λ1 og λ2 kalles Lagrange multiplikatorer. Uttrykket som vektorfelt (partiellderiverte)
\(\bigtriangledown f= \lambda_1 \bigtriangledown g_1 + \lambda_2 \bigtriangledown g_2\)
\(\bigtriangledown f= \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z},\right)\)
Funksjonen:
\(f(x,y)= x^2 - y^2\)
har et sadelpunkt:
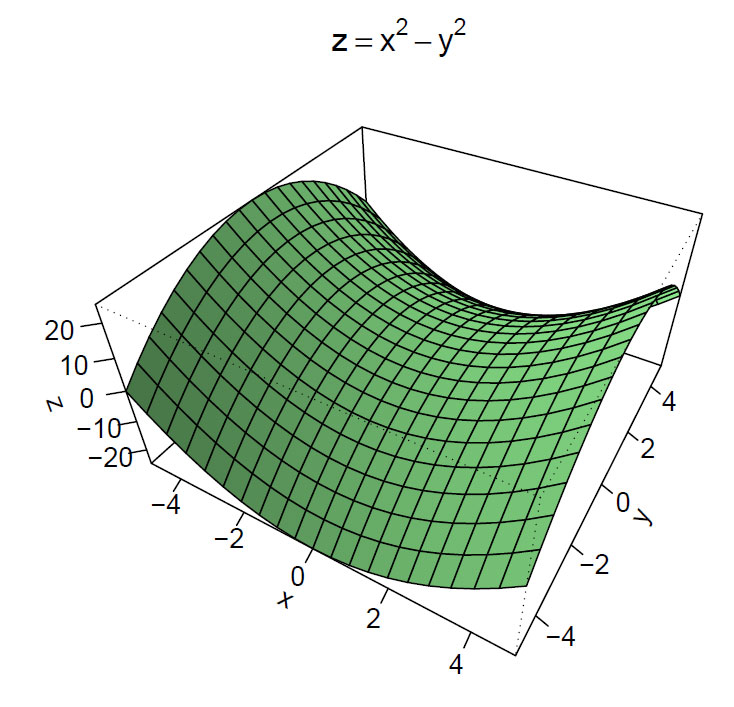
Et sadelpunkt blir det største blant de laveste punktene. I spillstrategi blir sadelpunktet den optimale strategi.
Eksempel 1
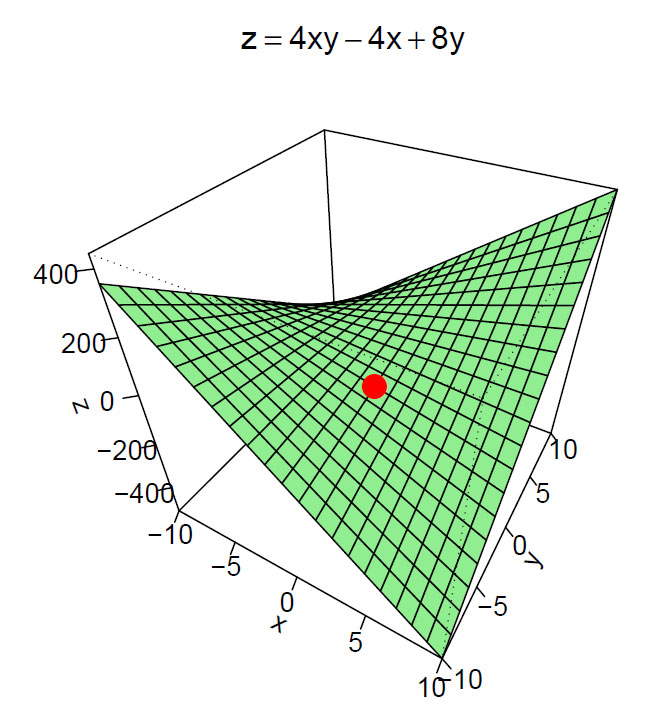
Vi skal finne maksimums- og minimumspunktene for funksjonen:
\(f(x,y)= 4xy-4x+8y\)
Vi ser at de partielle førstederiverte blir lik:
\(\displaystyle\frac{\partial f}{\partial x}= 4y-4\;\;\;\;\;\;\;\frac{\partial f}{\partial y}= 4x+8\)
Vi vil få et maksimums- eller minimumspunkt for de partielle førstederiverte er lik 0
\(4y-4=0 \;\;\;\;\;\;\; 4x+8= 0\)
Det vil si ved (1,-2). Men vi kan fremdeles ikke avgjøre om det er et maksimums- eller minimumspunkt. Vi kan plotte funksjonen, og det ser ut fra denne til å være et et sadelpunkt. Det kan imidlertid være vanskelig å se hvis det er flere dimensjoner, og vi må etter hvert finne en annen metode for å avgjøre om det er maks- eller minimumspunkt.
Tidligere har vi brukt den andrederiverte (andrederiverttesten) slik at når den førstederiverte f’(a)=0 så er a et lokalt minimum hvis den andrederiverte er større enn 0 (f’’(a)>0) og et lokalt maksimum hvis den andrederiverte er mindre enn 0 (f’’(a)<0). Hvis den andrederiverte er lik 0 (f’’(x)) så kan vi ikke avgjøre noe.
Vi kan lage en tilsvarende test for funksjoner ved flere variable.
Vi kan lage en Hesse-matrise H(f) (Ludwig Otto Hesse (1811-1874, en kvadratmatrise med de partielle andrederiverte til en funksjon f(x1,x2,…,xn):
\(\displaystyle H(f)= \begin{pmatrix} \frac{\partial ^2 f}{\partial x_1^2}& \frac{\partial ^2 f}{\partial x_1\partial x_2}& \cdots& \frac{\partial ^2 f}{\partial x_1\partial x_n}\\ \frac{\partial ^2 f}{\partial x_2\partial x_1}& \frac{\partial ^2 f}{\partial x_2^2}& \cdots& \frac{\partial ^2 f}{\partial x_2\partial x_n}\\ \vdots& \vdots &\ddots& \vdots\\ \frac{\partial ^2 f}{\partial x_n\partial x_1}& \frac{\partial ^2 f}{\partial x_n \partial x_2}& \cdots& \frac{\partial ^2 f}{\partial x_n^2} \end{pmatrix}\)
Hesse-matrisen er symmetrisk. Det betyr at Hesse-matrisen H(f(a)) i punktet a har n relle egenverdier λ1(a),λ2(a),…λn(a).
Hvis alle fortegnene til egenverdiene er positive har vi et minimum, er alle negative har vi et maksimum, og har egenverdiene både negative og positive fortegn har vi et sadelpunkt.
Det viser seg at Hesse-matriser er koeffisienten til kvadrat-leddet i Taylor rekkeutvikling av funksjonen (Taylors formel), hvor også Jakobi-matrisen inngår.
\(\displaystyle y=f (x + \Delta x)= f(x) + \bigtriangledown f(x) \Delta x+ \frac{1}{2}\left(H(f(x + c \Delta x) \Delta x\right)\Delta x\)
Skalarfeltet \(\bigtriangledown f(x)\)er det samme som Jakobi-matrisen, c=[0,1], Δx er en søylevektor, hvor både matriseprodukt og skalarprodukt inngår.
Vi kan se på funksjonen over med to variable. Da har vi en Hesse-matrise:
\(\displaystyle H(f(x,y))= \begin {pmatrix} \frac{\partial ^2 f}{\partial x^2} & \frac{\partial ^2 f}{\partial x \partial y}\\ \frac{\partial ^2 f}{\partial y \partial x} & \frac{\partial ^2 f}{\partial y^2} \end{pmatrix}\)
Da blir determinanten D til Hessematrisen:
\(\displaystyle D\left(H(f)\right)= \begin{vmatrix} A & B\\ B& C \end{vmatrix}= AC- B^2\)
Vi kan nå se på fortegnet på determinanten for å avgjøre hvilken type maks-min punkt vi har.
Hvis D<0 så er a et sadelpunkt
Hvis D>0 og A>0 så er a et minimumspunkt
Hvis D>0 og A<0 så er a et maksimumspunkt
Vi har to egenverdier til matrisen λ1 og λ2 og vi har at determinanten er produktet av egenverdiene:
\(D(H(f))= \lambda _ 1 \lambda _ 2\)
Fortegnene til egenverdiene avgjør også fortegnene til determinanten. Har de to egenverdiene likt fortegn blir determinanten større enn 0 (D>0). Har egenverdiene motsatt fortegn blir determinanten mindre enn 0 (D<0) og vi har et sadelpunkt.
Vi går tilbake til eksemplet ovenfor hvor vi fant:
\(\displaystyle\frac{\partial f}{\partial x}= 4y-4\;\;\;\;\;\;\;\frac{\partial f}{\partial y}= 4x+8\)
Hessematrise og de partielle andrederiverte:
\(A= \displaystyle \frac{\partial ^2 f}{\partial x^2}= 0\;\;\;\;\;\;B= \displaystyle \frac{\partial ^2 f}{\partial x \partial y}= 4\;\;\;\;\;\; C= \displaystyle \frac{\partial ^2 f}{\partial y^2}= 0\;\;\)
Vi lager en matrise av de partielle andrederiverte og finner determinanten til Hesse-matrisen:
\(\begin {vmatrix} 0 & 4\\ 4& 0 \end{vmatrix}\)
Egenverdiene (-4 og 4) og egenvektorene til Hessematrisen:
0.7071068 -0.7071068
0.7071068 0.7071068
Determinanten=AC - B2= -16
Vi ser at egenverdiene har motsatt fortegn, og determinanten til Hessematrisen er mindre enn 0, altså er punktet vi har funnet et sadelpunkt.
Eksempel 2:
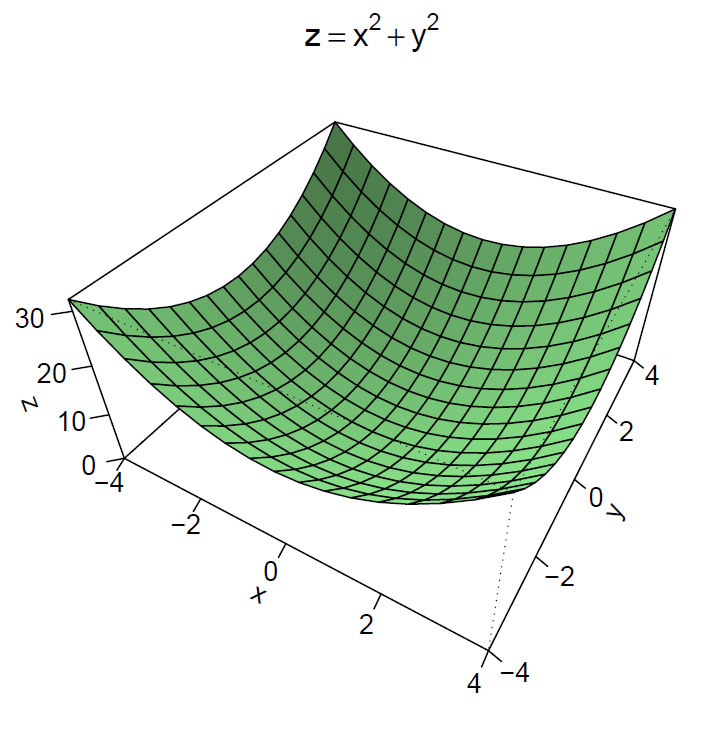
En enkel kvadratisk funksjon med to variable er:
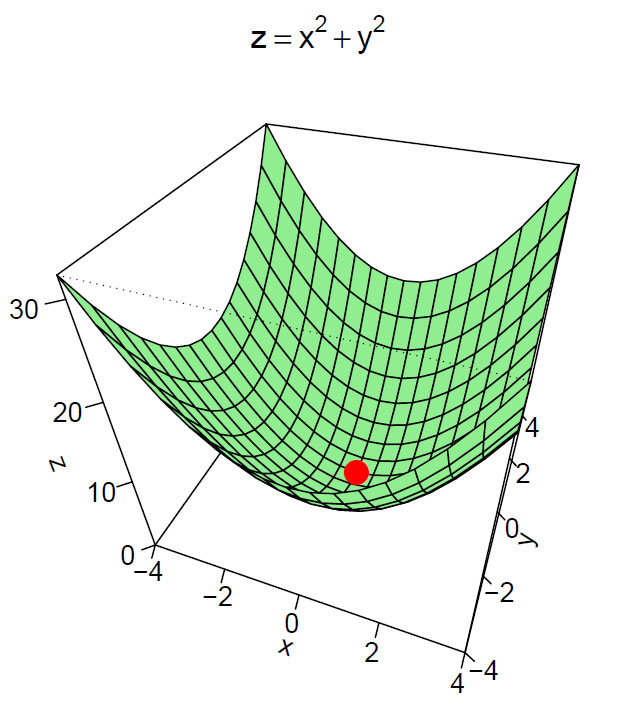
\(f(x,y)= x^2 + y^2\)
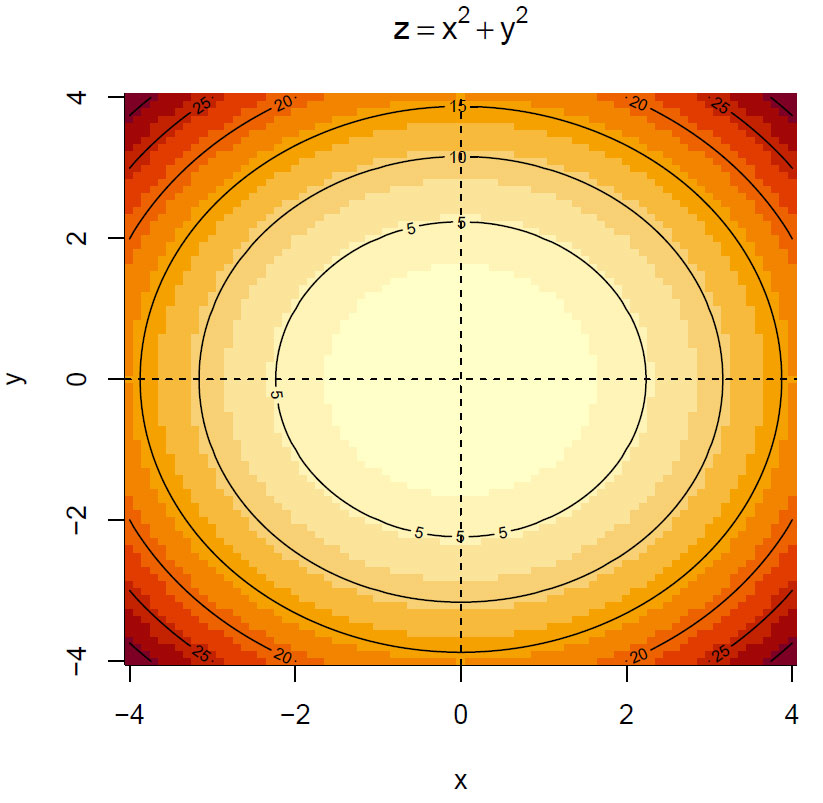
Vi finner de partiellderiverte:
\(\displaystyle\frac{\partial f}{\partial x}= 2x\;\;\;\;\;\;\; \frac{\partial f}{\partial y}= 2y\)
Vi setter begge de partiellderiverte lik 0 og finner at det eneste punktet som tilfredsstiller dette er (0,0).
Vi skal avgjøre om det er et maksimums- eller minimumspunkt ved å se på Hesse-matrisen for de partielle andrederiverte og determinanten:
\(\displaystyle D\left(H(f)\right)= \begin{vmatrix} A & B\\ B& C \end{vmatrix}= AC- B^2\)
\(A= \displaystyle \frac{\partial ^2 f}{\partial x^2}= 2\;\;\;\;\;\;B= \displaystyle \frac{\partial ^2 f}{\partial x \partial y}= 0\;\;\;\;\;\; C= \displaystyle \frac{\partial ^2 f}{\partial y^2}= 2\;\)
Dette gir egenverdier 2 2, og egenvektorene:
0 -1
1 0
og determinanten til Hessematrisen er lik 4.
Vi ser at egenverdiene har samme fortegn, og det betyr at determinanten er større enn 0 og vi finner at determinanten til Hesse-matrisen er lik 4, hvilket betyr at (0,0) er et minimumspunkt. Vi kan plotte minimumspunktet på figuren: