Elliptiske kurver har generell form, hvor a og b er rasjonale tall eller heltall modulo et heltall n:
\(\displaystyle y^2 = x^3 + ax + b\)
Koordinatene (x,y) kan også være i kompleksplanet og lager en Riemann-flate. Elliptiske kurver blir anvendt innen algebraisk geometri og ble også anvendt av Andrew Wiles i løsningen av Fermats siste teorem.
Figuren nedenfor er en elliptisk kurve fra et kubisk polynom med uendelige mange løsninger:
\(\displaystyle y^2 = x \left(x-3\right) \left(x+32\right)\)
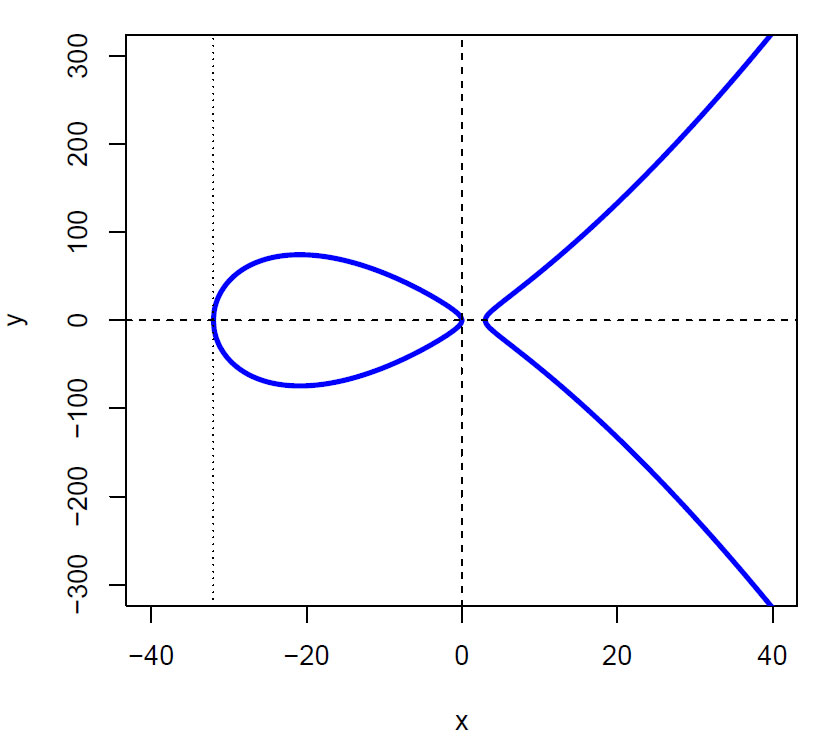
Ffiguren viser elliptisk kurve y2=x(x-3)(x+32). Kurven kan ikke krysse seg selv. Punkter på kurven kan summeres og gir et nytt punkt på kurven. Addisjonen danner en Abelsk gruppe hvor uendelig (∞) er et identitetselement (nullelement), Man kan beregne antall punkter (mod p) (modulær matematikk) på en elliptisk kurve ut fra Hasses teorem.
\(\displaystyle y^2 = x^3 + ax + b \pmod{n}\)
er par (x,y) (mod n) som tilfredsstiller ligningen modulo n, også ved uendelig

Figur elliptisk kurve Y2= x(x+1)(x-1)
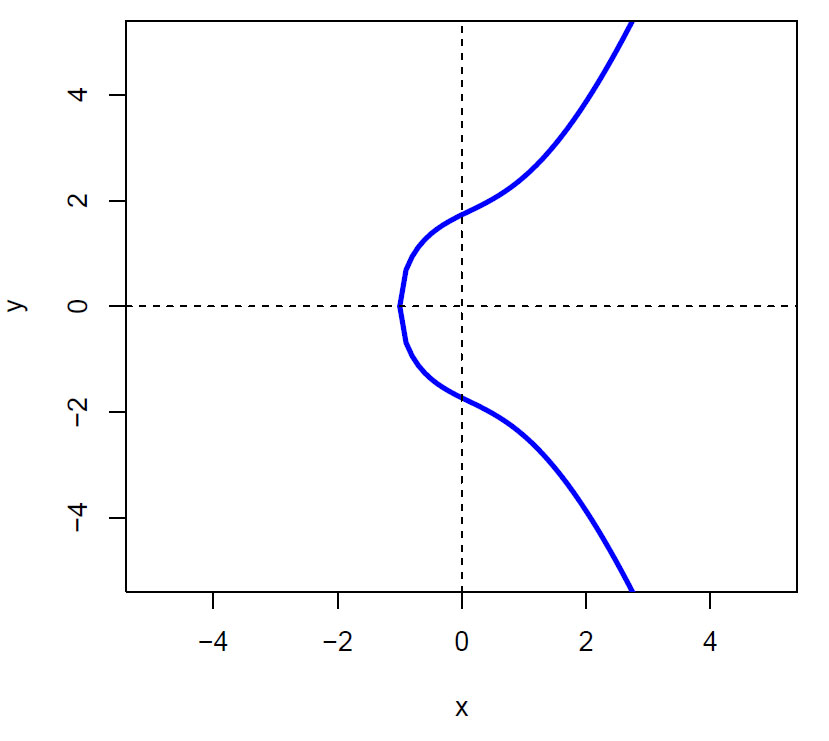
Figur elliptisk kurve Y2= x3+ 73
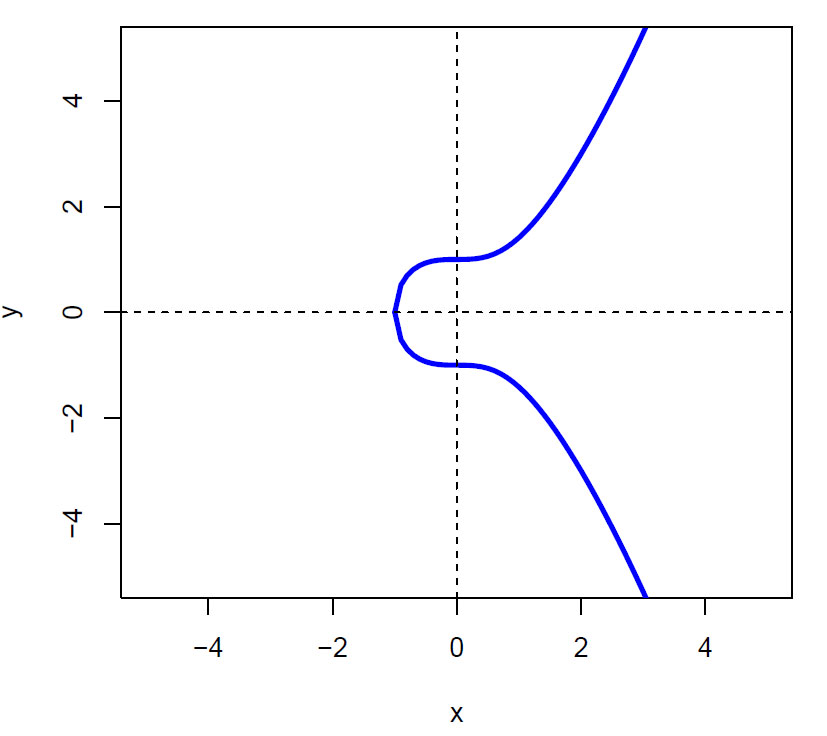
Figur elliptisk kurve Y2= x3+ 1
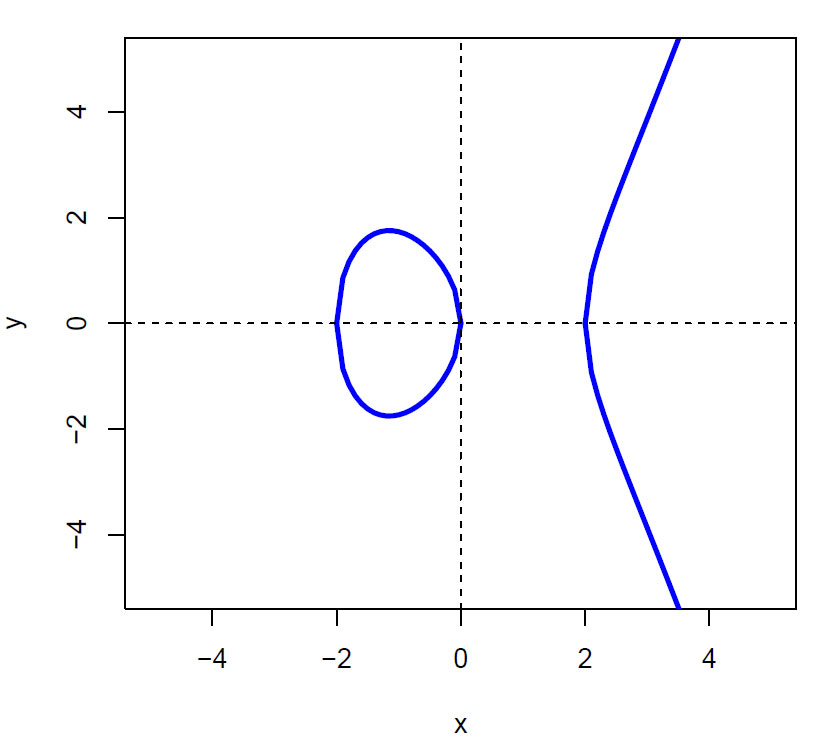
Figur elliptisk kurve y2= x3-4x.
Hvis man trekker en linje gjennom de to punktene P1 og P2 og denne skjærer linjen i den elliptiske kurven ved punktet Q(x,y) punkter så vil P1 + P2 = P3. Hivs linjen gjennom P1 og P2 er parallell med x-aksen så vil P1 + P2 = ∞
Hvis punktene P1 og P2 er like så er linjen en tangent til den elliptiske kurven og skjærer E i Q(x,y) så vil P1 + P1 = (x,-y).
Har man to punkter P1(x1,y2) og P2 (x2,y2) for en elliptiske kurve E
\(\displaystyle E: y^2 = x^3 + ax + b\)
så kan man summere disse og finne et punkt P3(x3,y3) på E ved følgende beregninger:
\(\displaystyle P_1 + P_2= P_3= \left( x_3, y_3 \right)\)
\(\displaystyle \alpha = \begin{cases} \frac{\left(y_2 - y_ 1 \right)}{\left(x_2 - x_1\right)} & \quad \text{hvis } P_1 \neq P_2\\ \frac{\left( 3x_1^2+a \right)}{\left(2y_1\right)} & \quad \text{hvis } P_1 = P_2\} \end{cases} \)
\(\displaystyle y_3= \alpha \left( x_1 - x_ 3 \right) - y_1\)
\(\displaystyle x_3 = \alpha^2 - x_1 - x_ 2\)
Både Euler og Lagrange undersøkte elliptiske integraler.
\(\displaystyle \int\limits_{x_1}^{x_2} \frac{dx}{\sqrt{x^3 + ax + b}}\)
Inne kryptografi velger Alice og Bob et primtall p på en elliptisk kurve E (E (mod p) og et punkt P (x,y) på den elliptiske kurven E. Alice velger et heltall na og beregner na P og Bob velger et heltall nb.og beregner nbP som de utveksler med hverandre. Deretter beregner Alice nanbP og Bob nbnaP og begge har nå samme nøkkel.
Isogenier mellom eliptiske kurver (ordinære eller supersingulære) anvendes i isogenibasert kryptografi. Gitt to elliptiske kurver E1 og E2 så finnes det en isogeni
f: E1→ E2
Supersingulære eliptiske kurver for primtall p er definert over et endelig felt Fp2. Det er ca. (p+1)/12 slike elliptiske kurver hvor to og to henger sammen med isogonier.