Franskmannen Pierre de Fermat (1601-1665) arbeidet med tallteori, infinitesimalregning, geometri basert på koordinater samt sannsynlighetsteori. Fermat brevvekslet med datidens store matematikere René Descartes (1591-1661), Blaise Pascal (1623-1662), John Wallis (1616-1703) og Gérard Desargues (1591-1661).
Fermat leste Diofantus Arithmetica, en av de første bøkene om algebra. Diofantus lette etter rasjonale tall x, y og z som løsning for den Pytagoreiske læresetningen:
\(x^2 + y^2 = z^2\)
I det Pytagoreiske triangel (trekant) som er rettvinklet og alle sidene har heltallslengder er det flere løsninger e.g. 32+42=52 eller 1192 + 1202 =1692 . Arealet av den rettvinklete trekanten blir 1/2xy.
Fermat viste at arealet av et triangel aldri kan bli lik arealet av et kvadrat. Man kan finne flere løsninger (Pytagoreisk trippel) ved å multiplisere med 2 e.g. 62+82=102. Hvis a, b og c er en Pytagoreisk trippel så vil ma, mb og mc være en Pytegoreisk trippel e.g. m=3 gir løsningstallene 9, 12 og 15.
Og motsatt: Hvis u, v og w er en Pytagoreisk trippel med d som en felles divisor, så vil u/d, v/d og w/d være en Pytagoreisk trippel.
Fermat utvidet den Pytagoreiske læresetningen videre, og Fermats store sats var at ligningen:
\(x^n + y^n=z^n\)
ikke har noen positive heltallsløsninger for de naturlige tallene n>2 (Ser bort fra å sette en av variablene lik 0). For n=2 er det flere løsninger (se over).

Fermat skrev i margen i Arithmetica at han hadde funnet beviset, men at det var for liten plass til å skrive det i margen. Et tema også nevnt i Stieg Larssons kriminalbøker om Lisbeth Salander. Fermat løste den selv for n=4, og Euler beviste den for n=3.
Den franske matematikeren Sophie Germain (1776-1831) studerte tallteori, og ga bevis for Fermats sats når n=5 , gjengitt i et vedlegg til andre utgave av Adrien-Marie Legendre sin bokThéorie des nombres. Germain ga også viktige bidrag i studiet av vibrerende elastiske overflater

Men hva med de andre tallene i den uendelige tallrekken ? Et fascinerende problem, selv en datamaskin kan ikke gå gjennom alle tall.

Andrew Wiles løsning av Fermats teorem gikk veien om Galois representering, modulære former med symmetri, eliptiske kurver, Hecke ringer, Kolyvagin-Flach-metoder, Eulersystemer, klassenummerformelen, Poincaré konjektur og Taniyama-Shimura konjektur.
Wiles trodde han hadde løsningen i 1994, den var imidlertid feil, vist av Nick Katz, men sammen med Richard Taylor kunne Wiles publisere beviset for Fermats siste sats i Annals of Matemathics i mai 1995.
Elliptiske kurver
Elliptiske kurver (elliptiske ligninger) har generell form:
\(y^2= x^3 + ax^2+bx + c\)
hvor a, b og c er reelle heltall, også kalt en Weierstrassligning.
Elliptiske kurver har et noe misvisende navn siden de ikke er ellipser. De ble først studert av Diofant i Aritmetica. Spørsmålet har vært om har de heltallsløsninger, og eventuelt hvor mange. En elliptisk kurve er en type kubisk kurve hvor løsningene er begrenset til en torus. En torus har form som en smultring. Elliptiske kurver er viktig innen tallteori.
Elliptiske kurver kryptografi baserer seg på de spesielle egenskapene ved eliptiske kurver og primtallsorden, men har i ettertid vist seg å være løsbar.
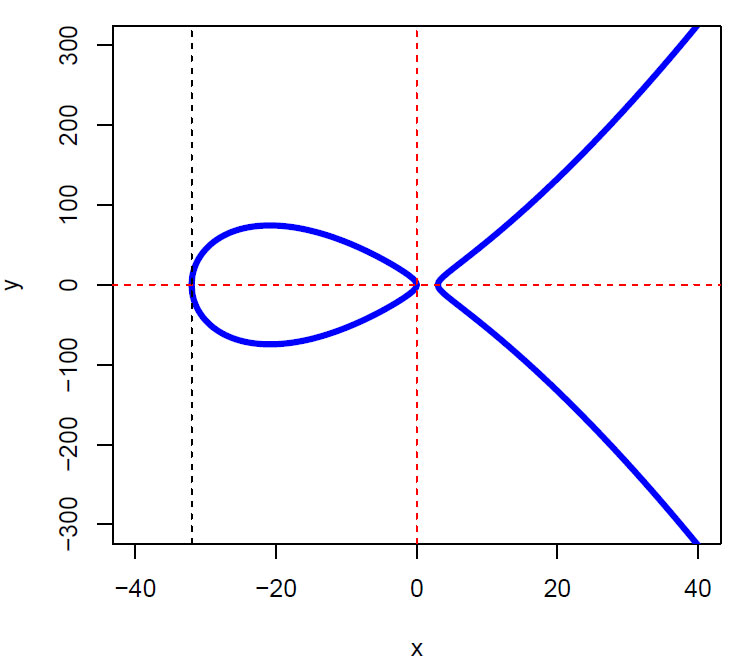
Figuren nedenfor er en ellliptisk kurve fra et kubisk polynom med uendelige mange løsninger:
\(y^2= x(x-3)(x+32)=x^3 + 29x^2-96 x\)
Fermat kunne vise at den elliptiske ligningen:
\(y^2=x^3-2\)
bare har en heltallsløsning x=3, 33 - 2= 52 =25. Dette er det eneste kvadratet og kube som har forskjell lik 2.
Den japanske matematikeren Yutaka Taniyama (1927-1958) fant på 1950-talleten kobling mellom to viktige deler av matematikken: elliptiske kurver og modulære former. Modulære former er funksjoner med imaginære tall (komplekse tall) som gir symmetri. Det viser seg at modulære former har uendelig mange symmetrier og kan derfor speiles, vris, roteres og snus. De modulære formene har to akser hvor begge aksene består av komplekse tall, hver med sin relle og imaginære akse, ,(xr, xi) og (yr, yi), noe som gir et firedimensjonalt rom (hyperbolsk rom), visualisert bla. i Eschers Circle limit IV eller Poincarés diskmodell. Poincaré hadde også studert modulære former og hadde blitt fascinert av deres symmetri.
Hyperbolsk geometri (Lobachevsky geometri) er ikke-Euklidsk geometri, og betyr bl.a. at parallelle linjer vil skjære hverandre. Jfr. sadelform, hyperbolske funksjoner, og summen av vinklene i en trekant blir mindre enn 180o. Nicolai Ivanovich Lobachevsky (1792-1856) viste at Euklids parallellaksiom holder ikke. I Einsteins generelle relativitetsteori er tidrommet ikke-Euklidsk. Store objekter med mye masse krummer tidrommet, jfr. gravitasjonskrefter, en relativt svak kraft, vi klarer å løfte en stein, og tyngdekraftensom virker over store avstander.
Enhver elliptisk kurve kan bli relatert til en modulær form, og er egentlig det samme vist av Gerhard Frey (Frey kurve) og Ken Ribet. Dette ble videreutviklet av Guro Shimura ca. 10 år seinere og oppdagelsen kalles Taniyama-Shimura konjekturen: til enhver elliptisk ligning svarer det en modulær form. For eksempel er magnetisme og elektrisitet deler av det samme. Frey mente at hvis Taniyama-Shimura konjekturen var sann, så kunne han også finne beviset for Fermats sats.
Gerhard Frey (1944-) viste at det måtte være en sammenheng mellom Taniyama-Shimura konjektur og Fermats siste sats. Frey (Frey kurve) omformet Fermats sats til følgende hvis han antok at Fermats sats var usann. Frey kom med påstanden at hvis Taniyama-Shimura formodningen ble bevist så hadde man samtidig bevist Fermats sats.
Ken Ribet ved Universitetet i California (Berkely) mente at siden enhver elliptisk kurve er modulær så vil følgelig Fermats sats ha ingen heltallsløsninger for n>2. Fra cn = an + bn kunne de vise at følger (Frey kurve)
\(y^2=x(x-a^n)(x-b^n)\)
En konjektur (også kalt formodning) brukes om en formel som man antar er riktig fordi den ikke er motbevist. Finner man et bevis for konjekturen blir den et teorem. Et annet eksempel på en konjektur er Poincaré-konjekturen. Modulære former finner man igjen bl.a. innen teoretisk fysikk innen strengteori (en oscillerende linje) som kobler kvantemekanikk og generell relativitet og danner basis for kvanteteorien for gravitasjon. Strengteorien er det nærmeste man i dag kommer ”teorien om alt” som kobler gravitasjon, elektromagnetisme, sterke og svake kjernekrefter, samt materie bestående av kvarker og leptoner. Fysikerne opererer med begreper som E8-matematikk (Lie-grupper (Sophus Lie)), 11-dimensjonal M-teori og supersymmetri.